
December 30, 2023
Nothing has fascinated the human mind quite like infinity. We use infinity to describe endless possibilities and express our desire to reach beyond our limited imagination. Throughout the history of civilization, that concept has pervaded throughout every facet of life, from literature to mathematics to the sciences and beyond. However, this blog post is not to add to that admiration of such a grand topic. Rather, I want to bring about a caveat that's rooted in engineering practice. In math, infinity is a limiting concept and it is defined rigorously; since in engineering we often construct mathematical models, we therefore encounter infinity on a regular basis. Therefore, it is crucial to know the ramifications of dealing with infinity in engineering as its misuse would defeat the very purpose of using models to deepen our understanding of a problem that engineering is trying to solve. Infinity is a mathematical curiosity but an engineering trap.
Engineers construct mathematical models to represent complex systems in hopes of simplifying them and predicting outcomes in this simplified environment using math, but that hope can only be realized if the models are applied correctly. In one of my earlier blog posts, I alluded to the famous quote by Statistician George Box: "All models are wrong, but some are useful." A mathematical model involves some sort of function that takes in inputs, namely the independent variables, and produces outputs, namely the dependent variables. While such a function might not capture all of the nuances of the system, it captures enough so that the output is close enough to that of the actual result such that it can be trusted to represent real-world behavior. Finally, when the real-world solution is implemented using the applications of such functions in a model, the real-world result hands down the final verdict as to whether the model was useful in the first place or not. Like natural selection, models that produce effective real-world solutions often survive to be used many more times throughout human history, while those that don't are quickly discarded.
This is where infinity comes in to disrupt the integrity of a mathematical model. Infinity, while being a rigorously-defined limiting concept in math, is often disregarded as "just another case" when that exact math is used in a model in engineering. The stereotypical example is black holes, where by using the corresponding complicated models which I won't attempt to recite, one emerges the concept of the "singularity". It is regarded as the center of the blackhole where the density becomes infinite. This presumably occurs because somewhere in the related function, a division by zero occurs, and many engineers equate division by zero to infinity. Hence, we are forced to imagine a region in spacetime with infinite density, and we are stuck. The presence of infinity and the subsequent emergence of an infinity singularity seriously jeopardizes the correct interpretation of the blackhole model. However, you might be thinking, "since no one can enter a black hole and come back to tell the tale, so who cares what the singularity looks like?"
Alright, so the Average Joe will likely never encounter a black hole, but certainly can experience "infinity" if "infinity" is treated as lightly as seen in the aforementioned case. In fact, let me take you on a journey to experience infinity! The first step is to take a trip to Target, or perhaps Amazon, or perhaps to any other department store/online etail site. The second step is to grab one of these:

Is that a portal to a black hole? No. It's a makeup mirror. If you've never used it before, let me briefly tell you how it works. The mirror sits on a swivel that can be flipped. On one side is the plane mirror that you are accustomed to. On the other side, however, is a concave mirror. If you sit right in front of the mirror facing the concave side, you will likely see the enlarged version of your face. This helps to facilitate putting on makeup, and hence the invention of the makeup mirror.
The concave mirror side is what we are interested in. Before going to the third step, however, I must provide some math that forms the mathematical model for concave mirrors.
Let's first give some names to our concave mirror setup:
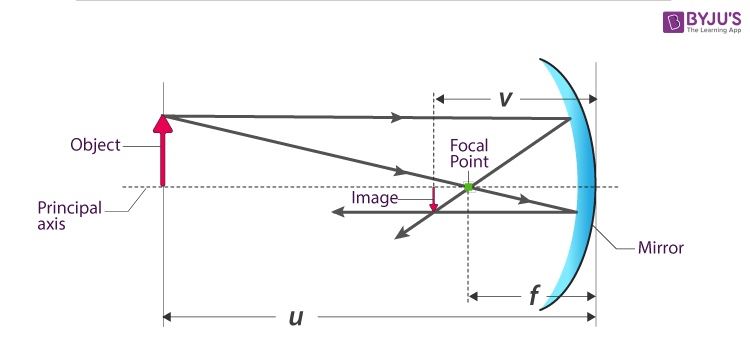
(Source: https://byjus.com/physics/mirror-equation/)
From the above diagram, \(u\) is the distance between the real object to the mirror, while \(v\) is the distance between the "virtual image", i.e. the image formed on the mirror. Don't worry about how to measure \(v\) here and I will just use "image" instead of "virtual" or "real" image from now on. Next, we have \(f\), which is called the focal length of the mirror and is in fact a fixed value dependent on one of the properties of the mirror, namely its curvature \(R\). That is:
\begin{align} f &= \frac{R}{2} \end{align}
The following are some equations tying the above variables together and are a result of the properties of light. If you are interested, you can try deriving them via geometry.
First, the relationship among \(f\), \(u\), and \(v\) is given as follows:
\begin{align} \frac{1}{f} &= \frac{1}{u} + \frac{1}{v} \end{align}
Then, the magnification of the virtual image, \(M\), is given as follows:
\begin{align} M &= -\frac{v}{u} \end{align}
\(M\) can be any real number. If \(M\) is negative, that means the image is flipped upside down as compared to the real object. The larger the magnitude of \(M\), the larger the magnification, and vice versa.
Now, as engineers, our job is to construct a mathematical model that ties \(M\) to how far the real object is from the mirror, i.e. \(u\). We use the above two equations for our task:
\begin{align} \frac{1}{f} &= \frac{1}{u} + \frac{1}{v} \\ \\ M &= -\frac{v}{u} \\ \\ v &= -Mu \\ \\ \frac{1}{f} &= \frac{1}{u} - \frac{1}{Mu} \\ \\ \frac{1}{f} &= \frac{1}{u}\left(1 - \frac{1}{M}\right) \\ \\ \frac{1}{M} &= 1 - \frac{u}{f} \\ \\ M &= \frac{1}{1 - \frac{u}{f}} \\ \\ M &= \frac{f}{f - u} \\\ \end{align}
Recall that \(f\) is fixed upon the shape of the concave mirror, our model for magnification is simply a function in terms of \(u\), the distance between the mirror and the real object, as desired.
\begin{equation} \boxed{M(u) = \frac{f}{f - u}} \end{equation}
Of course, in real life, the exact magnification might not behave like the above function. There could be imperfections on the mirror surface, or there could be scattering or dispersions or the fact that the mirror is not standing exactly upright. Nonetheless, we can appreciate the effectiveness of a model if it can remove all those complexities and focus on the core principles of the concave mirror, giving us a useful tool to predict what the virtual image would look like depending on where we place the real object in front of the mirror. Of course, the final verdict is always the real-world result, so let's predict and verify!
Let's say you are the object. As you start right next to the mirror and move back but always ensuring you are closer to the mirror than the focal length, what happens? When you touch your nose on the mirror, \(u\) can be considered 0, and so \(M(0) = 1\) and the mirror acts like a plane mirror. As you move back, \(u\) increases but is always less than \(f\). Therefore, \((f - u)\) decreases from the positive direction and getting closer and closer to 0. Since \(f\) is always positive, that means \(M\) remains positive and gets larger and larger, effectively enlarging your face without flipping the image. Therefore, it achieves its intended purpose of helping you put on makeup (or examine your face more clearly).
Now let's consider the other side. Suppose you start just a bit further from the mirror than \(f\), and gradually move back even further. Here, \(u\) is always greater than \(f\), and so \((f - u)\) is always negative. Again, since \(f\) is always positive, that means \(M\) remains negative and therefore the image is always flipped. When \(u\) is close to \(f\), \((f - u)\) is a small (in magnitude) negative number close to 0, and so \(M\) is very large in magnitude. As you move back further, \(u\) increases, and so \((f - u)\) increases too in the negative direction. Since this is on the denominator with \(f\) fixed, that means \(M\) gets smaller and smaller in magnitude the further you move back, with the image in the mirror always flipped.
Now let's put our mathematical model to the mettle by subjecting it to the most stringent test: reality. Grab the makeup mirror you just obtained and repeat the conditions described above and verify that the predictions from our model indeed matches your observations. If it does, then that means our model successfully represents the magnification of the concave mirror, and we can finally move on to the next step in our journey to reach infinity!
The third step is the final step to observe "infinity": make yourself exactly the focal length distance away from the mirror. Why? Because from our model, which you verified is an effective and useful one, when we set \(f = u\), we get a division by zero. However, as engineers, that means we get infinity, right? So whatever we see in the mirror is the face of infinity, literally!
\begin{align} M(f) &= \frac{f}{f - f} = \frac{f}{0} = \infty \\ \end{align}
This is the engineering trap. Engineers prize practicality. We need math to make predictions to solve problems on complex systems, but we gloss over intricate mathematical concepts along the way as we eagerly reap the fruits of our models. However, doing so would let the concept of infinity turn our models against us as we draw incorrect conclusions from such cases. For our concave mirror, I find it especially fascinating because the "flip" happens for some value of \(u\). When \(u\) is less than \(f\), the image is upright, and when \(u\) just exceeds \(f\), the image is flipped. Unlike traveling to a black hole, this point of "infinity" can easily be observed by anyone. Simply place the makeup mirror on a table and position yourself next to the mirror. Then, slowly move back. You will see your face gets larger and larger and then, poof, it flips! Now you are upside down inside the mirror and getting smaller and smaller as you continue moving backwards.
So let's talk about the "flip". You may not know the exact value of \(f\), but you can play around with your mirror and estimate where it might be by the image when it is just about to "flip". At \(u = f\), what do you see in the mirror? Let's see what ChatGPT has to say:


In summary, ChatGPT correctly analyzes the model at the point \(u = f\), and by correctly I mean extending the behavior of the model to that infinity point. It mentions that the reflected rays are now parallel and the virtual image forms at "infinity" (ah that cursed word!).
But does the image flips at \(u = f\)? What do you actually see in the mirror? I encourage you to check it out. In the meantime, there is a simple explanation to all this mess:
Dividing by zero is undefined, not infinity.
Yes, in fact \(M(f)\) is actually undefined. That means the model fails to predict what happens at that point. It could be that no image forms, or some other model is needed to explain what is observed in reality. The point is, we have to put on our math hat for a moment and consider the nuanced distinction between \(M(f)\) and infinity. In math, infinity is a limiting concept, and limits are well defined using delta-epsilon. In summary, it means that I can attain any arbitrarily large number for \(M\) in magnitude either from the positive side or from the negative side by adjusting \(u\) to be arbitrarily close to \(f\), but never equal to \(f\). Indeed, one-sided limits for \(M(u)\) as \(u\) approaches \(f\) exists and is equal to \(\pm \infty\), but the rigorous definition of limits in math asserts that \(u\) can never be at \(f\) exactly. In our case, if \(u = f\), we have a division by zero and in fact our model becomes undefined. When \(u \neq f\), no matter how close the two values get, our model is always well defined and can produce the desired outcome.
The following applet illustrates the scenario well and I encourage you to play with it. Here I placed the real object pretty much at \(f\), the focal point of the mirror, and the simulation shows parallel rays with no image on the other side of the mirror, as ChatGPT analyzed earlier. However, compare this with reality and see if you see something happening in the mirror at \(f\).
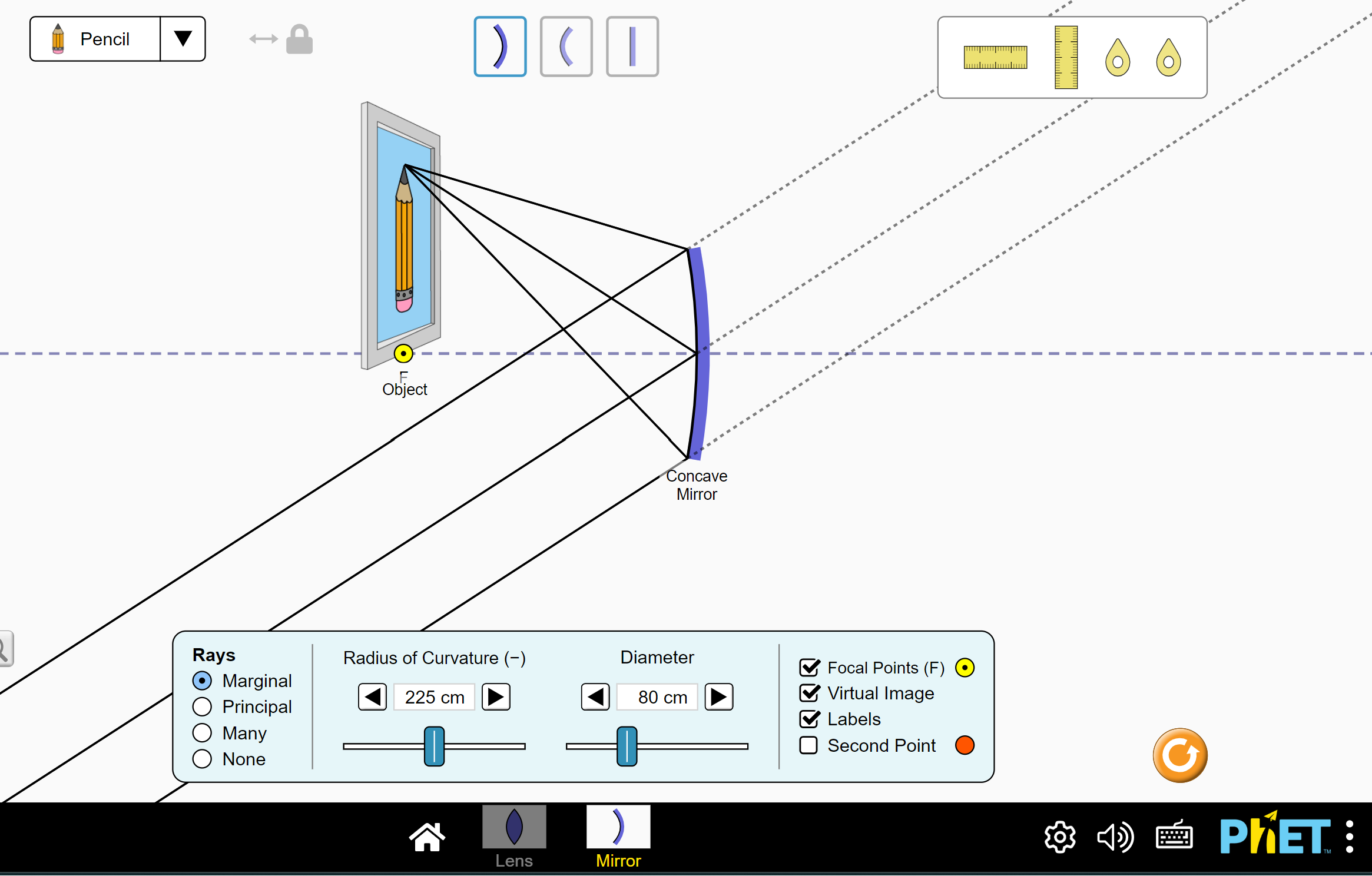
(Source: https://phet.colorado.edu/sims/html/geometric-optics/latest/geometric-optics_all.html)
From our model, the magnification at \(u = f\) should be infinity. It still doesn't answer when exactly the "flip" happens. Some online tutorials say that at the focal point, the image is inverted, while others say it's not. Furthermore, the prevalent characterization of the image is that it is simply "highly enlarged", as seen here:

(Source: https://www.youtube.com/watch?v=Hp0PsU6mUGs&ab_channel=InfinityLearnNEET)
However, "highly enlarged" still implies a finite magnification, which runs in contradiction with what the model is predicting at that point. The way to resolve it is to realize that division by zero doesn't yield infinity, it yields "undefined". When a model is "undefined" at an input, we cannot use it to predict any corresponding outputs.
I hope this brief journey to experience infinity does not diminish the concept's allure, but rather serves as a cautionary tale to ensure that it is treated with care where it arises in mathematical models. As engineers, if we leverage mathematical models to help us solve complex problems, we can't just take the model and leave the math--we must take both so that we don't become ensnared inside the infinity trap.
By the way, just by sheer coincidence, the above YouTube channel is named "Infinity Learning NEET". Looks like the concept of "infinity" is really ubiquitous. Also, this channel, at the time of writing, has about \(\pi\) million subscribers!