Gambler's Cranberry Sauce

David Ding

November 27, 2020

Well folks, it is the day after Thanksgiving. I hope all of my dear readers had a safe, happy, and stomach-satisfying Thanksgiving whichever way you guys have celebrated. To those of you who chose to put off physically being with your family this year, please accept my sincere gratitude. You guys are true selfless heroes who deserve a big round of applause from everyone, and when we celebrate an especially heart-warming Thanksgiving in 2021, you guys will be a big reason for this accomplishment.

This blog post was inspired by one of my readers who Emailed me about my previous post, where I presented my solution to the Riddler Classic problem: Can You Pass The Cranberry Sauce?. Special thanks to Prof. Henk Tijms from the University of Amsterdam for taking the time to read my blog posts and sharing a wonderful insight into the Cranberry Sauce problem. In his Email response to me, he brought up an alternate analysis to the Cranberry Sauce problem as a different "Chairman Selection" problem in his book Surprises in Probability- Seventeen Short Stories which I am delighted to check it out. In the meantime, Prof. Tijms mentioned the use of the "Gambler's Ruin" formula to solve the Chairman Selection problem, and a lightbulb went off my head.

Gambler's Ruin. The first thing that popped into my head seeing this was that I probably can use my blog to post a PSA:

Gambling can ruin your life. Run away from it and don't touch it ever.

Coincidentally, my blog has been concentrated on various quirks in math, so here, why not try to use math to prove the above adage? Heck, the name "Gambler's Ruin" probably spoils the ending on whether gambling pays (answer: No!), but what is the mysterious formula that is the "Gambler's Ruin", and how does that tie into the Cranberry Sauce problem?

A Different Kind of Table

Let's gamble on something, just to see how it pays. Here, instead of gambling on money, we are going to gamble on--the Cranberry Sauce (sorry if you are already sick of it from the Thanksgiving meal). We do so by modifying the original Cranberry Sauce problem through the kind of table you are sitting for the meal. Instead of a circular table, it is going to be rectangular, with you along with, let's say N other friends and familiy members this time, all sitting in a line. You will be person 0, the person to your right is person 1, the person to person 1's right is person 2, and so on, until person N all the way at the other end of the table.

To start off, you have the cranberry sauce, and after helping yourself, you pass the sauce to person 1 on your right. Each person thereafter has a probability of $0 \leq p \leq 1$ of passing the sauce to his/her right, and therefor probability $q = 1 - p$ of passing back to his/her left. However, for some reason, you are in a very grumpy mood and swear that you will NOT be passing the sauce twice. If you get back the sauce somehow, you will dump it all in the trash can. Okay, maybe you'll receive some scolding from your mother along the table, but for the sake of argument, let's pretend this is the scenario.

What is the probability that the cranberry sauce will make its way down to person N?

You can see how this parallels a gambler. The gambler plays a game where he/she starts off with $1, and wants to win $N in the end. Each time he/she plays the gambler can either win $1 or lose $1. When he/she loses everything, the gambler's day is done (ruined!). What is the probability that the gambler will reach $N?

The setup is like the following Markov Chain:

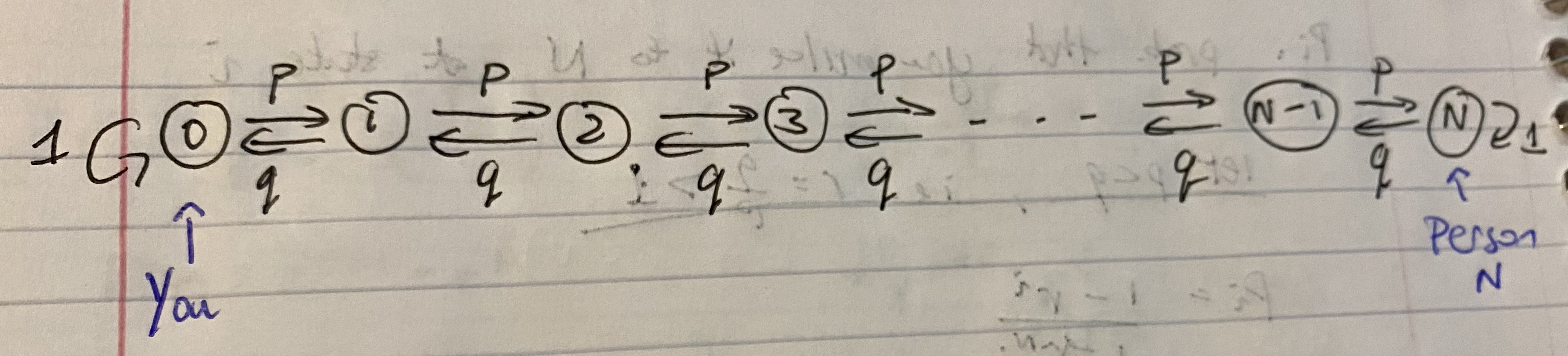
Don't worry if you are not familiar with the concept of Markov Chains. The reason why I bring up this model is to highlight an important observation in solving this problem. When say person 2 receives the cranberry sauce, it doesn't matter if that person received it in two passes or 30 passes; the moment person 2 receives the sauce (before person N has received it, of course), the game resets. Everything that happened before person 2 received the sauce does not matter anymore. If we denote the probability that person N will eventually receive the sauce when currently person $i$ has the sauce as $P_{i}$ (note the capital P here), then $P_{i}$ does not depend on what happened before person $i$ got the sauce. Such systems are called memoryless systems, in which Markov Chains excel at modelling them. So from the perspective of person 2, below is the stochastic chart of the cranberry sauce journey, starting from person 1:

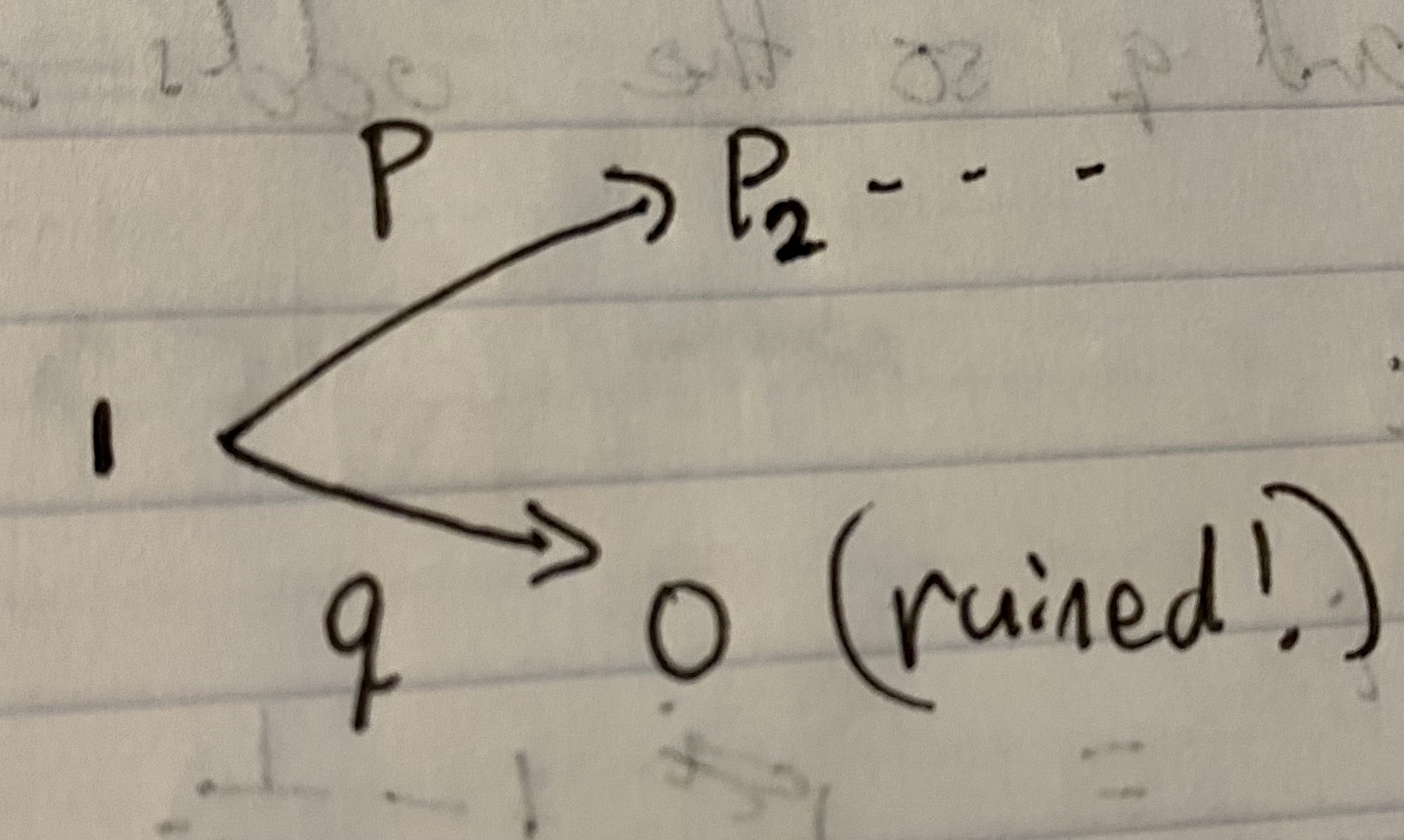
The stochastic chart above is not complete, of course, because when the sauce reaches person 2 the journey continues, with ultimately probability $P_{2}$ that it will reach person N. However, the key is to highlight the two distinct paths that the sauce takes once person 1 has it. Either the sauce gets passed back to the grumpy "you", i.e. person 0, in which case the sauce meets the trash can, or it reaches person 2 and the journey continues. By our setup, the sauce has a probability $p$ of reaching person 2 and a probability of $q = 1 - p$ of going to person 0 and thereby meeting its doomed fate.

From the above stochastic chart, we have the following relationship based on the Law of Total Probability:

$P_{1} = p P_{2} + q P_{0}$

Let me translate the above equation into English: the probability of the cranberry sauce reaching person N while person 1 currently has it, denoted as $P_{1}$ , is if it reaches person 2 with probability $p$ , in which case it would then have a probability $P_{2}$ of reaching person N, and, if it reaches person 0 with probability $q$ , in which case it would then have a probability $P_{0}$ of reaching person N.

But what is $P_{0}$ ? Clearly $P_{0} = 0$ by our scenario setup: once you receive the sauce again, it won't be going to anyone else but the trash can. Similarly, $P_{N} = 1$ : mission accomplished!

So we really just have: $P_{1} = p P_{2}$

But what is $P_{2}$ ? Since if person 2 has the sauce, the sauce can only travel back to person 1 or advance to person 3, we only need to involve 1 and 3 into our equation for $P_{2}$ , in a similar fashion: $P_{2} = p P_{3} + q P_{1}$

Remember, $p$ is the probability of advancing the sauce and $q = 1 - p$ is the probability of retreating it.

So we have a system of equations, one for each state: $\begin{aligned} P_{0} & = 0 \\ P_{1} & = p P_{2} \\ P_{2} & = p P_{3} + q P_{1} \\ P_{3} & = p P_{4} + q P_{2} \\ P_{4} & = p P_{5} + q P_{3} \\ \dots \\ P_{i} & = p P_{i + 1} + q P_{i - 1} \\ \dots \\ P_{N - 1} & = p P_{N} + q P_{N - 2} \\ P_{N} & = 1 \end{aligned}$ Our goal here is to find a formula for $P_{i}$ . At the first glance, we might have too many variables to work here, but note how each successive equation contains adjancent variables from the previous equation. I smell telescoping here.

$\begin{aligned} P_{i} & = p P_{i + 1} + q P_{i - 1} \\ p P_{i} + q P_{i} & = p P_{i + 1} + q P_{i - 1} \\ q P_{i} - q P_{i - 1} & = p P_{i + 1} - p P_{i} \\ P_{i + 1} - P_{i} & = \frac{q}{p} (P_{i} - P_{i - 1}) \end{aligned}$

Look at the last equation: we have a series of differences for $i - 1$ , $i$ , and $i + 1$ . This is great for telescoping. Let's write out what the above equation entails. Hereafter we will let $r = \frac{q}{p}$ . $\begin{aligned} P_{2} - P_{1} & = r (P_{1} - P_{0}) \\ P_{3} - P_{2} & = r (P_{2} - P_{1}) \\ P_{4} - P_{3} & = r (P_{3} - P_{2}) \\ \dots \\ P_{i + 1} - P_{i} & = r (P_{i} - P_{i - 1}) \\ \dots \\ P_{N} - P_{N - 1} & = r (P_{N - 1} - P_{N - 2}) \end{aligned}$

So now after we add up the above equations, all but the end terms on both sides of the equations cancel out! We can even choose not to add up to N and only add up to the first $i$ equations and obtain: $P_{i} - P_{1} = r (P_{i - 1} - P_{0})$

In particular, we know that $P_{0} = 0$ , and so $P_{2} - P_{1} = r P_{1}$ . Continue our previous system of equations leads to $P_{3} - P_{2} = r (P_{2} - P_{1}) = r \times r P_{1} = r^{2} P_{1}$ . Essentially, every equation in our previous system can be written as only in terms of $r$ and $P_{1}$ : $\begin{aligned} P_{2} - P_{1} & = r (P_{1} - P_{0}) = r P_{1} \\ P_{3} - P_{2} & = r (P_{2} - P_{1}) = r^{2} P_{1} \\ P_{4} - P_{3} & = r (P_{3} - P_{2}) = r^{3} P_{1} \\ \dots \\ P_{i + 1} - P_{i} & = r (P_{i} - P_{i - 1}) = r^{i - 1} P_{1} \\ \dots \\ P_{N} - P_{N - 1} & = r (P_{N - 1} - P_{N - 2}) = r^{N - 1} P_{1} \end{aligned}$

Putting everything together, we obtain: $P_{i} - P_{1} = P_{1} (r + r^{2} + r^{3} + \dots + r^{i - 1})$

Look at this! We've got ourselves a geometric series! But we have to be careful. When r = 1, we don't need the geometric series formula, but rather recognizing that we have $i - 1$ copies of r:

For $r = 1$ , $\begin{aligned} P_{i} - P_{1} & = P_{1} (i - 1) r \\ P_{i} & = P_{1} (i - 1) r + P_{1} \\ P_{i} & = P_{1} i r \\ P_{i} & = i P_{1} \end{aligned}$ We note that when $i = N$ , $P_{i} = 1$ , and so substituting: $\begin{aligned} P_{N} & = N P_{1} \\ 1 & = N P_{1} \\ P_{1} & = \frac{1}{N} \\ P_{i} & = \frac{i}{N} \end{aligned}$

For $r \neq 1$ , we can use the geometric series formula: $\begin{aligned} P_{i} - P_{1} & = P_{1} (r + r^{2} + r^{3} + \dots + r^{i - 1}) \\ P_{i} & = P_{1} (1 + r + r^{2} + r^{3} + \dots + r^{i - 1}) \\ P_{i} & = \frac{1 - r^{i}}{1 - r} P_{1} \end{aligned}$ Again, we note that when $i = N$ , $P_{i} = 1$ , and so substituting: $\begin{aligned} P_{N} & = \frac{1 - r^{N}}{1 - r} P_{1} \\ 1 & = \frac{1 - r^{N}}{1 - r} P_{1} \\ P_{1} & = \frac{1 - r}{1 - r^{N}} \\ P_{i} & = \frac{1 - r^{i}}{1 - r} \frac{1 - r}{1 - r^{N}} \\ P_{i} & = \frac{1 - r^{i}}{1 - r^{N}} \end{aligned}$

So in summary, $P_{i} = {\begin{cases} \frac{1 - r^{i}}{1 - r^{N}}, p \neq \frac{1}{2} \\ \frac{i}{N}, p = \frac{1}{2} \end{cases}$ The above formula is the "Gambler's Ruin formula". The parameters are as follows:

$N$ : desired end state.
$i$ : current state.
$p$ : probability of advancing to the next state.

And the output, $P_{i}$ , denotes the probability that the cranberry sauce will eventually reach person N, giving that it is currently in the hands of person i, with probability that person i will pass the sauce down the table with probability $p$ .

Visualizing Gambler's Ruin

Like the probability of the last person receiving the sauce skewing wildly with different values of $p$ from the Riddler problem, here I am simulating using Matlab the various values of $p$ and see the fraction of times the sauce reaches person N = 20 starting with person i. For each case, the simulation amount is 10,000 trials. I am also plotting alongsied the theoretic probability from the Gambler's Ruin formula to show you guys how it compares with empirical data. I will be attaching the simulation code at the end of my post for you to play around yourself.

Starting with $p = \frac{1}{2}$ :

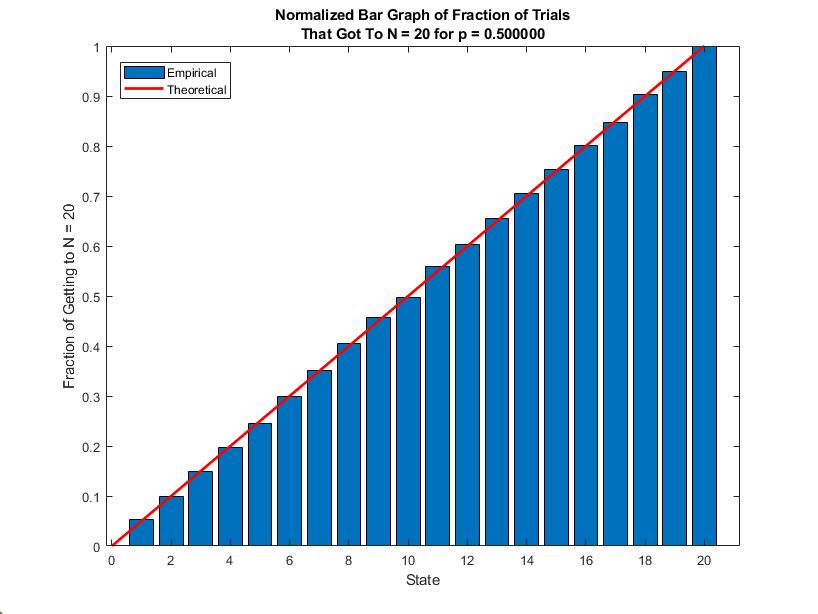
For $p = \frac{1}{2}$ , the Gambler's Ruin formula is a linear function, and we get a nice "staircase" empirical data set. From the start, the cranberry sauce has a $\frac{1}{20}$ probability of reaching person 20. If the sauce makes it halfway to person 10, then it will be 10 times more likely to reach person 20 then at the start with person 1.

Things start to skew when we increase $p$ to gambler's favor:

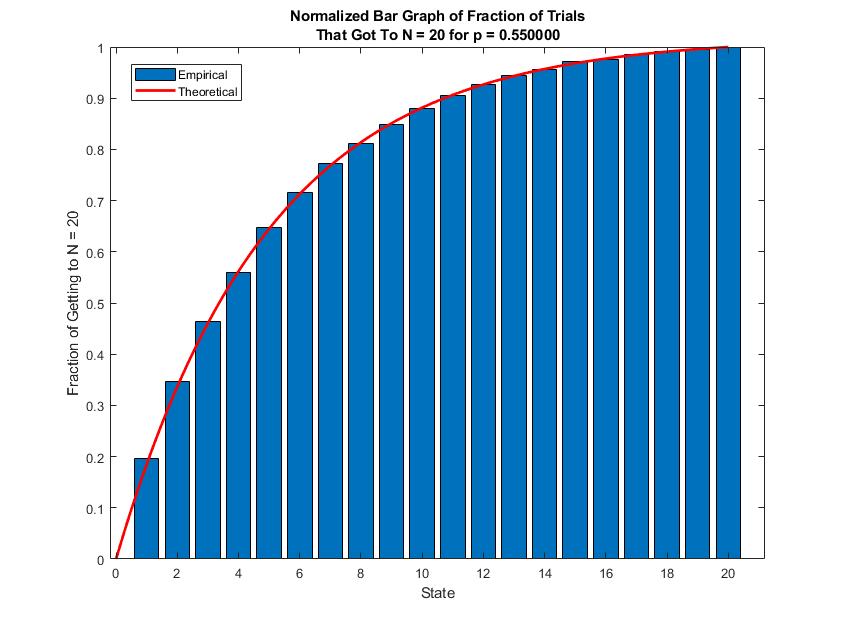
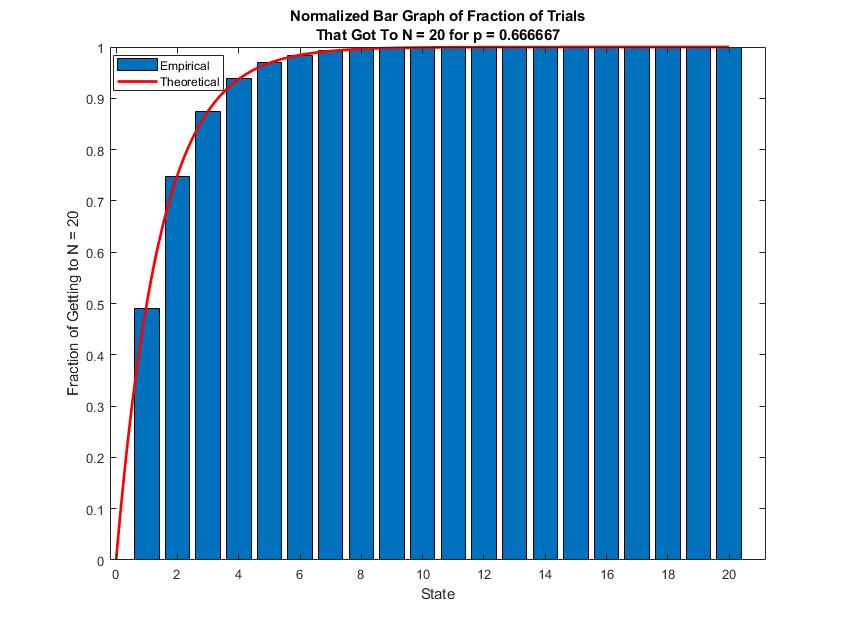
The Gambler's Ruin formula becomes concave when $p > \frac{1}{2}$ and how quickly so. Even increasing just 5 percentage points in the favor of the gambler makes it much more likely for person N to eventually reach person N. In fact, the cranberry sauce is expected to reach person 20 with probability $\frac{1}{5}$ , or four times as likely as when $p = \frac{1}{2}$ ! This mirrors the highly sensitive skewing of the cranberry sauce passing from the last Riddler problem.

On the other hand, when gambler's fortune is not in his/her favor, via $p < \frac{1}{2}$ , we get a different story:

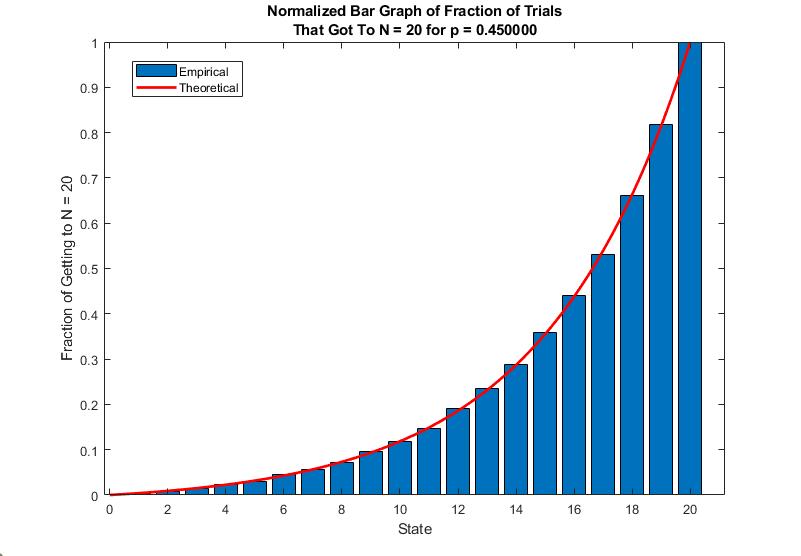
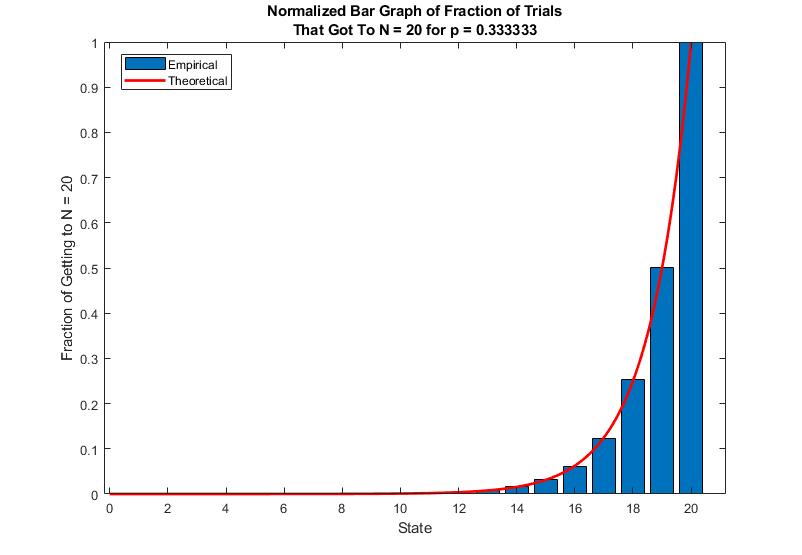
The Gambler's Ruin formula becomes convex when $p < \frac{1}{2}$ , but other than this, the story is pretty much the same--the skewness is highly sensitive to deviations from $p = \frac{1}{2}$ . When $p = \frac{1}{3}$ , you'd have the sauce make its way to person 13 (somehow) just to have a glimpse of hope of reaching person 20! Just swaying the probability against the gambler by mere 5 percentage points means that there is a whopping 20% chance, yes, 20%, that the sauce will not make it to person 20 even if it has reached person 19.

Gambling Doesn't Pay

If we let $N \to \infty$ , we get the following for the Gambler's Ruin formula: $P_{i} = {\begin{cases} 1 - r^{i}, p > \frac{1}{2} \\ 0, p \leq \frac{1}{2} \end{cases}$ The above result is obtained from the fact that when $p > \frac{1}{2}$ , $0 < \frac{1 - p}{p} = r < 1$ , and so when we take the limit as $N \to \infty$ for our Gambler's Ruin formula, we arrive at the above result...

...Which gets back to my PSA: Gambling Doesn't Pay. What the above Gambler's Ruin formula tells us, in plain English, is that even if the odds of winning a hand in blackjack, or winning the slot machine each time you pull it, is stacked in your favor, which, you'd be dreaming if you can find a casino that actually does, you will still only have a chance at striking it rich. If the stack is not in your favor, which is the reality in all casinos, you have a certainty that you will lose everything you gamble in the long run. Odds in your favor? You may get rich from gambling. Odds even or not in your favor? You will lose everything from gambling. That is the Gambler's Ruin.

Epilogue: Symmetry

But wait, you might ask, how can this be? Shouldn't the probability of one reaching the goal of striking riches (getting a large $N value) be just as certain for $p > \frac{1}{2}$ as going bankrupt for $p \leq \frac{1}{2}$ ? After all, looking at our Markov Chain from the start:

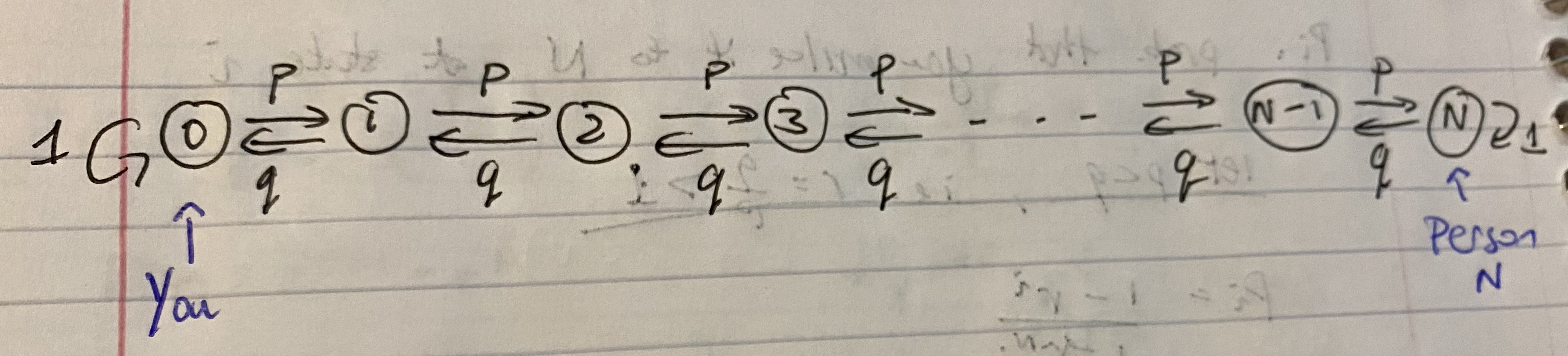
There seems to be a symmetry displayed between states 0 and N. If I switch those states, or if I switch p and q, then should I obtain the exact same scenario?

Not quite. To see this, we will use math as our definitive judge. We are going to look at two values here. The first value is $1 - P_{i}$ , which is the probability that you will go bankrupt while at state $i$ , except, here let's make going bankrupt our goal. This is akin to switching states 0 and N. The second value we are looking at is switching up p and q. This means that our original $r$ becomes $\frac{1}{r}$ in this case. If the scenario is truly symmetric, then the two values should be equal.

Without loss of generality, let our original $r > 1$ . That is, in the original scenario, the odds are stacked against the gambler. Then, our first value measures how likely the gambler will go bankrupt, which here we will define as "success", which is the likelier of the two long-term scenarios since the odds are against him/her. The second value then measures how likely the gambler will succeed given switched p and q, in which case the odds will be in his/her favor. In either case, both switched scenarios are in the gambler's favor, and if the symmetry argument holds, they should yield equal values.

First Value

The first value is $1 - P_{i}$ . Using Gambler's Ruin, we get: $\begin{aligned} 1 - P_{i, (original)} & = 1 - \frac{1 - r^{i}}{1 - r^{N}} \\ = \frac{1 - r^{N} - 1 + r^{i}}{1 - r^{N}} \\ = \frac{r^{i} - r^{N}}{1 - r^{N}} \\ = \frac{r^{N} - r^{i}}{r^{N} - 1} \\ = \frac{r^{N + i} - r^{2 i}}{r^{i} (r^{N} - 1)} \end{aligned}$ In the last step I multiplied the fraction by $\frac{r^{i}}{r^{i}}$ . You will see why soon.

Second Value

The second value is when we switched p and q such that $r$ becomes $\frac{1}{r}$ . Using Gambler's Ruin again, we get: $\begin{aligned} P_{i, (new)} & = \frac{1 - {(\frac{1}{r})}^{i}}{1 - {(\frac{1}{r})}^{N}} \\ = \frac{1 - \frac{1}{r^{i}}}{1 - \frac{1}{r^{N}}} \\ = \frac{r^{i} - 1}{r^{i}} \frac{r^{N}}{r^{N} - 1} \\ = \frac{r^{N + i} - r^{N}}{r^{i} (r^{N} - 1)} \end{aligned}$ Notice that the expression for the second value has the same denominator as the first value, hence the reason I multiplied the expression for the first value by $\frac{r^{i}}{r^{i}}$ .

Comparing the Two Values

So we have two values: $1 - P_{i, (original)}$ when we switched states 0 and N and $P_{i, (new)}$ when we switched p and q. How do those two values compare? ${\begin{cases} 1 - P_{i, (original)} = \frac{r^{N + i} - r^{2 i}}{r^{i} (r^{N} - 1)} \\ P_{i, (new)} = \frac{r^{N + i} - r^{N}}{r^{i} (r^{N} - 1)} \end{cases}$ And remember we let $r > 1$ and so the denominator in both cases will be greater than 0. From direct inspection, we can see that the two values are NOT equal. We can set them equal by setting $i$ in terms of $N$ , which we can do: $\begin{aligned} \frac{r^{N + i} - r^{2 i}}{r^{i} (r^{N} - 1)} & = \frac{r^{N + i} - r^{N}}{r^{i} (r^{N} - 1)} \\ r^{N + i} - r^{2 i} & = r^{N + i} - r^{N} \\ r^{2 i} & = r^{N} \\ 2 i & = N \\ i & = \frac{N}{2} \end{aligned}$

So here's the punchline, symmetry can be exploited when you are at the halfway point between losing everything and reaching your goal. However, in the endless pursuit of riches, $N$ usually is a large amount, and so even $\frac{N}{2}$ is no small amount to ignore. When people start to gamble, they usually have a pretty big $N$ as their dream but not the $\frac{N}{2}$ to begin achieving it. When the condition for symmetry is not there, and one gambles with $r > 1$ , in other words the odds are stacked against them, which usually is the case, instead what the gambler gets is:

$\begin{aligned} i & < \frac{N}{2} \\ 2 i & < N \\ r^{2 i} & < r^{N} \\ r^{N + i} - r^{2 i} & > r^{N + i} - r^{N} \\ \frac{r^{N + i} - r^{2 i}}{r^{i} (r^{N} - 1)} & > \frac{r^{N + i} - r^{N}}{r^{i} (r^{N} - 1)} \\ 1 - P_{i, (original)} & > P_{i, (new)} \end{aligned}$

What the above inequality tells us is that when you gamble with less than sufficient amount to start with, the chances of you going bankrupt is greater than making it even with reversed odds stacked in your favor. There is no symmetry here. Maybe if you are a tycoon and you start the gambling with a large enough fund and with seasoned advisers making sure your goal isn't too ambitious, then you might increase your worth through gambling. However, in even the slightest realistic scenario, you will lose everything. Gambling truly doesn't pay.

Simuluation Code

Please find the Simulation Code here.