Riddler Classic: February 3, 2022

David Ding

February 3, 2022

Beer Makes You Forget

Explanation:

We are going to assume that if you have forgotten which verse you are on, you always start over, regardless of whether you are on the last verse or not. You only truly finish if you've sang "1 bottle of beer on the wall" and you remember it's only 1 bottle left. We are also assuming that each verse is equally likely to have the beer count forgotten, and each sing-along produce the same forgetting tendencies (i.e. no sing-along runs are special).

With those assumptions out of the way, time to solve the puzzle! We will focus on the first part for now, which is the one with 99 beers. The key is to realize that once you start over, whether you make it to the end without forgetting is completely independent of your previous runs. Therefore, we make use of two random variables here: \(X\) and \(Y\). \(X\) represents in any given run, how many verses you've sang before you sang the verse where you forgot the beer count, and \(Y\) represents the number of failed runs before your next run that completes the sing-along. The key to solving the problem is to figure out:

1. On average, how many verses do you sing before you forget the beer count for a failed run? Let that number be \(E[X | failed run]\).
2. On average, how many failed runs are there? That number is represented by \(E[Y]\).

The total number of verses you would sing on average would then be:

\begin{align} \text{Average Total Verses} &= (E[X | \text{failed run}] + 1) E[Y] + 99 \\ \end{align}

Let's look at \(X\) first. Assuming that you are equally likely to forget any of the verses, let's denote that probability of forgetting as \(p\). In this problem, \(p = 0.01\) as given. Remember, \(X\) represents the number of verses you've sang BEFORE you sang the verse where you forgot the beer count. For example, if \(X = 73\), that means while singing the 74th verse (i.e. "26 bottles of beer..."), you forgot the count. The next verse would be "99 bottles of beer". Now, for simplicity, let \(X\) be able to take on values of \(0, 1, 2, 3, \dots, 99, \dots\) and up to infinity. That way, the event that you did NOT forget the beer count and do a successful run would be equivalent to \(X \ge 99\), i.e. you've sang 99 verses before the next one that you would forget, but of course, there is no next verse so you've completed the song. With this assumption, it is also clear that if the probability of forgetting each verse is independent and equally likely of one another, then \(X\) has a geometric distribution with parameter \(p = 0.01\).

We now calculate \(E[X | \text{failed run}]\). Intuitively, this expression, based on the definition of expectation, our defined events of a successful run, and the PDF of geometric distributions should be:

\begin{align} & E[X | \text{failed run}] \\ \\ &= \sum_{x = 0}^{98} x P(X = x) \\ \\ &= \sum_{x = 0}^{98} x (1-p)^x p \\ \end{align}

But it is not correct! This is because \(X\) can take on values of integers beyond 98, all the way to infinity. The expectations we calculate is only partial up to 98, and therefore is not the full expectation with the given condition. Luckily, since we assume that each verse is equally likely to be forgotten, we can just normalize the above expression by \(P(\text{failed run})\), which is just \(1 - (1 - p)^{99}\).

Now, let's denote \(q = 1 - p\). We first calculate :

\begin{align} &\sum_{x = 0}^{98} x q^x p \\ \\ &= p \sum_{x = 1}^{98} x q^x = pq \sum_{x = 1}^{98} x q^{x-1} \\ \\ &= pq \sum_{x = 0}^{98} (q^x)' = pq \left(\sum_{x = 0}^{98} q^x\right)' \\ \\ &= pq \left(\frac{1 - q^{99}}{1 - q}\right)' \\ \\ &= pq \left(\frac{1 - 99 q^{98} + 98 q^{99}}{(1 - q)^2}\right) \\ \\ &= q \left(\frac{1 - 99 q^{98} + 98 q^{99}}{p}\right) \end{align}

Putting everything together, we have:

\begin{align} & E[X | \text{failed run}] \\ \\ &= \frac{\sum_{x = 0}^{98} x q^x p}{1 - q^{99}} \\ \\ &= \left(\frac{q}{p}\right) \left(\frac{1 - 99 q^{98} + 98 q^{99}}{1 - q^{99}}\right) \\ \end{align}

Plugging in \(p = 0.01\) and therefore \(q = 0.99\) yields:

\begin{align} E[X | \text{failed run}] &= \boxed{40.9246}\\ \end{align}

This means that on average, given a failed run, you expect to sing about 41 verses before forgetting the count while singing the 42nd verse. So in total, you sing around 42 verses per failed run given 99 verses in total.

Now let's focus on \(Y\), which is the random variable representing the number of failed runs before the next run is successful. Clearly, as we assume that each run is i.i.d, \(Y\) also has a geometric distribution with probability of success \(h\) representing the probability of a successful run. Since we can have as many runs as possible before having a successful run, \(Y\) can take on values of \(0, 1, 2, \dots\) all the way to infinity.

We can calculate \(h\) as simply \(P(X \ge 99)\). This is simply equal to the probability that all 99 verses are remembered:

\begin{align} h &= P(X \ge 99)\\ \\ &= q^{99} \\ \\ &\approx 0.3697\\ \end{align}

We can directly calculate \(E[Y]\) as:

\begin{align} E[Y] &= \frac{1 - h}{h}\\ \\ &\approx \boxed{1.7047} \\ \end{align}

Which means that on average, you would be singing 2.7 rounds.

Using our formula for calculating the average verses to sing earlier, we have:

\begin{align} &\text{Average Total Verses} \\ \\ &= (E[X | \text{failed run}] + 1) E[Y] + 99 \\ \\ &= (40.9246 + 1) \times 1.7047 + 99 \\ \\ &= \boxed{170.4679} \end{align}

I wrote a Monte-Carlo simulation to see if our theoretical answer makes sense. Below is the sing-along code written in MATLAB:

function totVerses = singBeerSong(numVerses, probForget)
    % Get total number of verses sung in one trial
    % via Monte-Carlo

    totVerses = 0;

    nextVerse = 1;
    while nextVerse <= numVerses
        totVerses = totVerses + 1;
        
        forget = rand() < probForget;
        if forget
            % start over
            nextVerse = 1; 
        else
            % move on to the next verse
            nextVerse = nextVerse + 1;
        end
    end
end

Plugging in "numVerses = 99" and "probForget = 0.01" with 10 million Monte-Carlo trials yielded the simulated average number of verses to be 170.4441, which is only 0.014% away from theory.

General Formula

Before tackling the Extra Credit, let us derive a general formula for the average verses as a function of total number of verses and probability of forgetting the beer count on any given verse, keeping the same assumptions aforementioned. Let that value be \(f(N, p)\) where \(N\) is the number of verses and \(p\) is the probability of forgetting. The top-down approach first yields the formula as:

\begin{align} f(N, p) &= (E[X | \text{failed run}] + 1) E[Y] + N \\ \end{align}

Where \(X\) is the random variable representing how many verses were sung where you remember the beer count (and forgetting it while singing the next verse). \(X = 0, 1, 2, \dots\). \(Y\) is the random variable representing how many failed runs occur before the next run completes the sing-along. The intuitive explanation is that during your failed runs, you sing on average \((E[X | \text{failed run}] + 1)\) verses. On average, you have \(E[Y]\) failed runs. Then, the next run is successful, and you sing \(N\) verses in that run.

For ease of calculation, we let \(X\) take on all non-negative integer values. This allows us to model \(X\) using geometric distribution with parameter \(p\). Of course, when accounting for average verses sung in a failed run, we need to normalize the expectation for \(X = 0, 1, 2, \dots N - 1\) by the probability that the run is a failure, which is justified since each verse is equally likely to have the beer count forgotten. Letting \(q = (1 - p)\), this means:

\begin{align} & E[X | \text{failed run}] \\ \\ &= \frac{\sum_{x = 0}^{N - 1} x q^x p}{1 - q^{N}} \\ \end{align}

We can evaluate the numerator with some derivative calculus tricks:

\begin{align} &\sum_{x = 0}^{N-1} x q^x p \\ \\ &= p \sum_{x = 1}^{N-1} x q^x = pq \sum_{x = 1}^{N-1} x q^{x-1} \\ \\ &= pq \sum_{x = 0}^{N-1} (q^x)' = pq \left(\sum_{x = 0}^{N-1} q^x\right)' \\ \\ &= pq \left(\frac{1 - q^{N}}{1 - q}\right)' \\ \\ &= pq \left(\frac{1 - N q^{N-1} + (N-1) q^{N}}{(1 - q)^2}\right) \\ \\ &= q \left(\frac{1 - N q^{N-1} + (N-1) q^{N}}{p}\right) \\ \end{align}

Therefore:

\begin{align} & E[X | \text{failed run}] \\ \\ &= \frac{\sum_{x = 0}^{N - 1} x q^x p}{1 - q^{N}} \\ \\ &= \left(\frac{q}{p}\right) \left(\frac{1 - N q^{N-1} + (N-1) q^{N}}{1 - q^{N}}\right) \\ \end{align}

Now, for \(E[Y]\), we note that \(Y\) is also geometrically distributed, but with parameter \(h = P(\text{successful run}) = q^N\). No normalization is needed here and \(E[Y]\) is simply:

\begin{align} E[Y] &= \frac{1-h}{h} \\ \\ &= \frac{1 - q^N}{q^{N}} \\ \end{align}

Putting everything together, we have:

\begin{align} f(N, p) &= (E[X | \text{failed run}] + 1) E[Y] + N \\ \\ f(N, p) &= \left[\left(\frac{1 - p}{p}\right) \left(\frac{1 - N (1-p)^{N-1} + (N-1) (1-p)^{N}}{1 - (1-p)^{N}}\right) + 1 \right] \left[\frac{1 - (1-p)^N}{(1-p)^{N}}\right] + N \\ \end{align}

Below is the graph validating the above theoretical formula with Monte-Carlo simulation, keeping \(N = 99\) but varying \(p\):

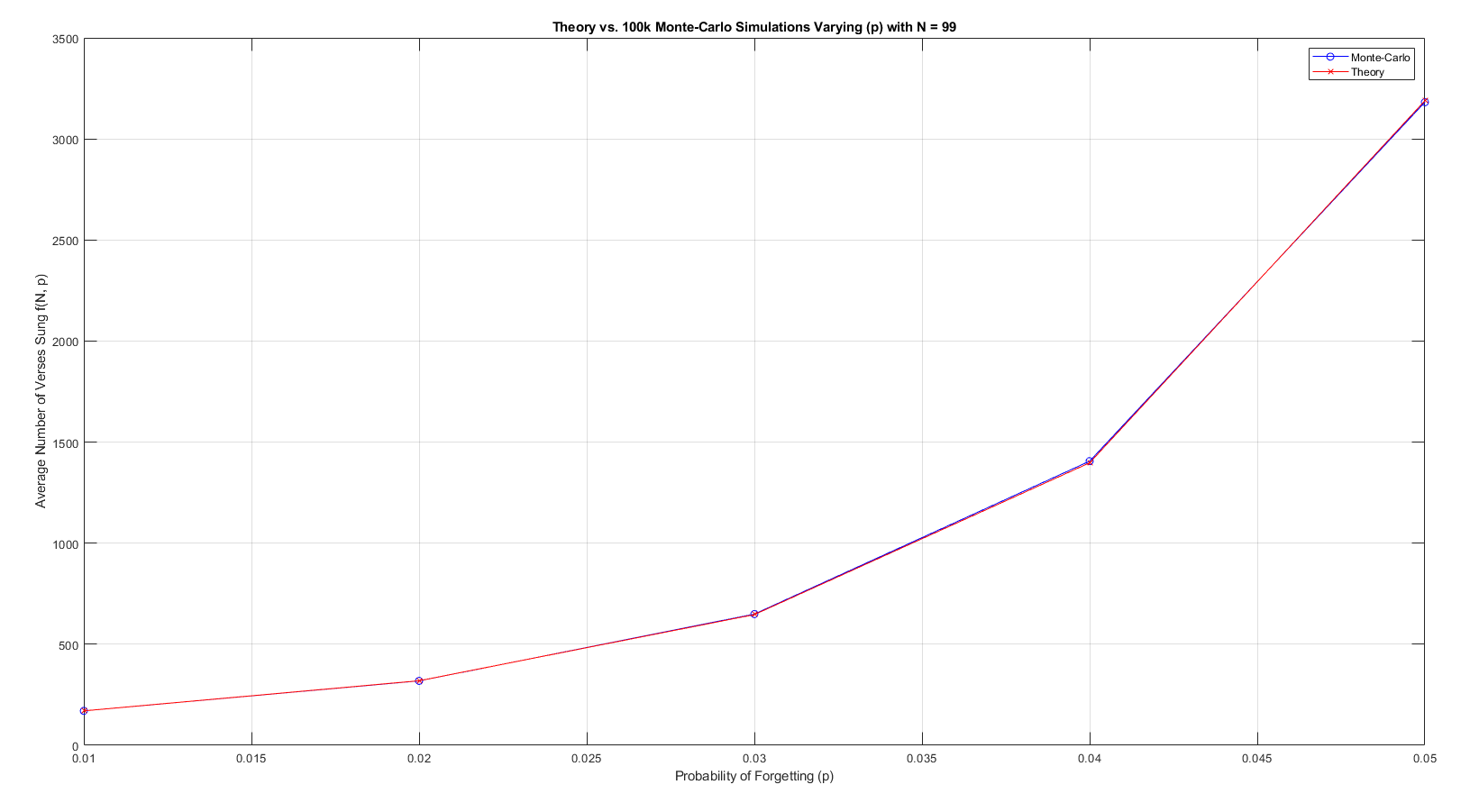
Even with only a 5% chance of forgetting a particular verse, on average one will sing over 3000 verses. This is a more than 30 times blow-up of the minimum verses needed to be sung.

Now let's keep \(p = 0.01\) and vary \(N\):

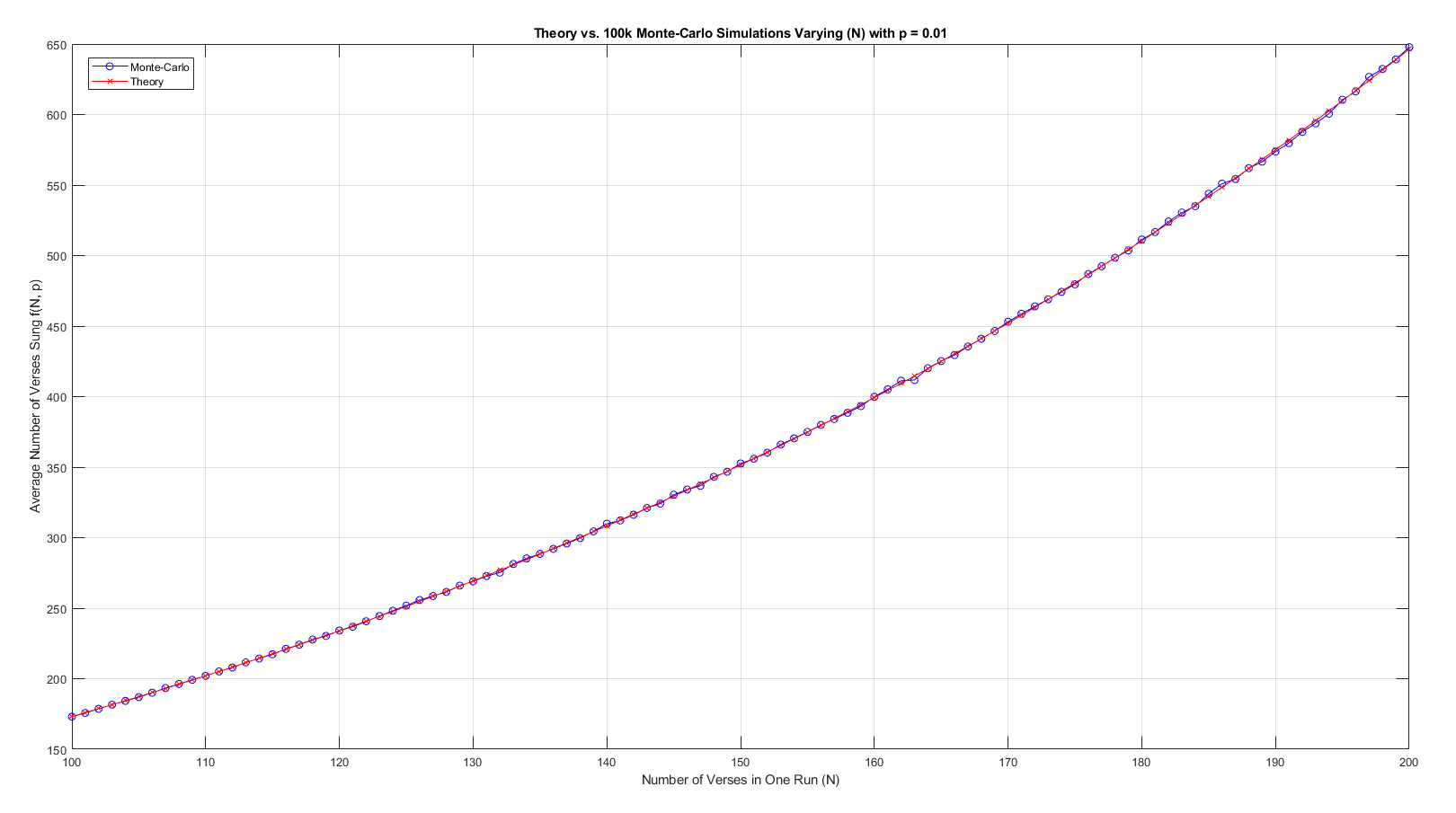
The increase in \(f(N, p)\) is more modest with \(N\) than that with \(p\). For 200 verses in one song, we only expect to sing around 650 verses with 1% chance of forgetting any particular verse.

More importantly, it verifies that our theoretical formula makes sense. We can now use it for solving the Extra Credit!

Extra Credit

For the extra credit, we are asked, "Instead of "99 Bottles of Beer," suppose you and your friends are singing "N Bottles of Beer," where N is some very, very large number. And suppose your collective probability of forgetting where you are in the song is 1/N for each verse. If it takes you an average of K verses to finish the song, what value does the ratio of K/N approach?". We first run our theoretical formula and see what value the ratio converges, and then make some analysis from there.

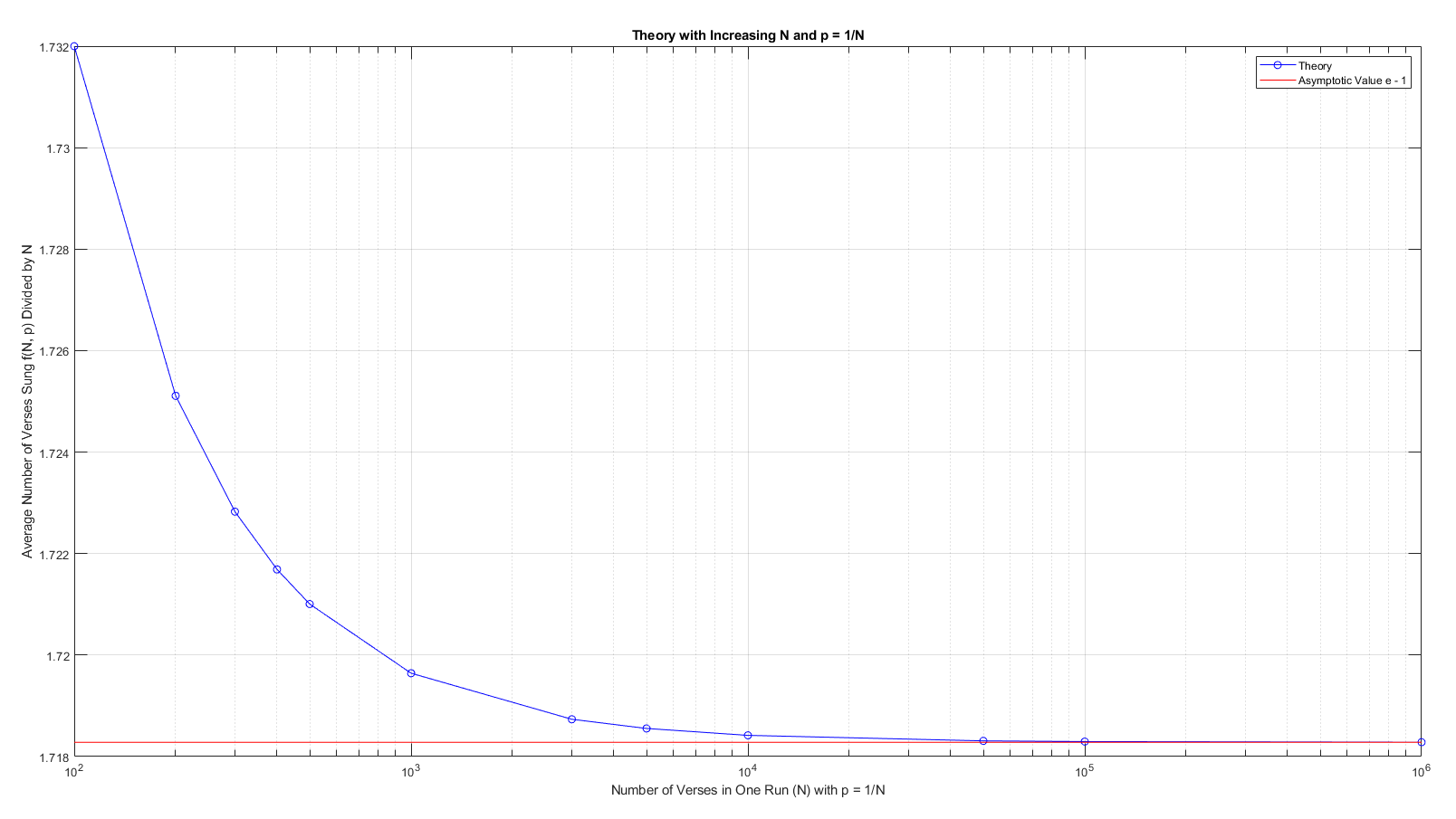
Here, I can't help but notice that the ratio converges to a very peculiar value: \(e - 1\). I will show it using the formula derived.

\begin{align} f(N, p) &= \left[\left(\frac{1 - p}{p}\right) \left(\frac{1 - N (1-p)^{N-1} + (N-1) (1-p)^{N}}{1 - (1-p)^{N}}\right) + 1 \right] \left[\frac{1 - (1-p)^N}{(1-p)^{N}}\right] + N \\ \\ g(N) &= \frac{f\left(N, \frac{1}{N}\right)}{N} = \frac{1}{N}\left[\left(\frac{1 - \frac{1}{N}}{\frac{1}{N}}\right) \left(\frac{1 - N \left(1-\frac{1}{N}\right)^{N-1} + (N-1) \left(1-\frac{1}{N}\right)^{N}}{1 - \left(1-\frac{1}{N}\right)^{N}}\right) + 1 \right] \left[\frac{1 - \left(1-\frac{1}{N}\right)^N}{\left(1-\frac{1}{N}\right)^{N}}\right] + 1 \end{align}

Our answer is \(\lim\limits_{N \to \infty} g(N)\). Before we evaluate this limit, let's simplify the expression for \(g(N)\) a little bit.

\begin{align} g(N) &= \frac{1}{N}\left[\left(\frac{1 - \frac{1}{N}}{\frac{1}{N}}\right) \left(\frac{1 - N \left(1-\frac{1}{N}\right)^{N-1} + (N-1) \left(1-\frac{1}{N}\right)^{N}}{1 - \left(1-\frac{1}{N}\right)^{N}}\right) + 1 \right] \left[\frac{1 - \left(1-\frac{1}{N}\right)^N}{\left(1-\frac{1}{N}\right)^{N}}\right] + 1 \\ \\ &= \frac{1}{N}\left\{\left[\left(\frac{1 - \frac{1}{N}}{\frac{1}{N}}\right) \left(\frac{1 - N \left(1-\frac{1}{N}\right)^{N-1} + (N-1) \left(1-\frac{1}{N}\right)^{N}}{1 - \left(1-\frac{1}{N}\right)^{N}}\right)\right] \left[\frac{1 - \left(1-\frac{1}{N}\right)^N}{\left(1-\frac{1}{N}\right)^{N}}\right] + \frac{1 - \left(1-\frac{1}{N}\right)^N}{\left(1-\frac{1}{N}\right)^{N}}\right\} + 1 \\ \\ &= \frac{1}{N}\left\{\left[\left(\frac{1 - \frac{1}{N}}{\frac{1}{N}}\right) \left(\frac{1 - N \left(1-\frac{1}{N}\right)^{N-1} + (N-1) \left(1-\frac{1}{N}\right)^{N}}{\left(1-\frac{1}{N}\right)^{N}}\right)\right] + \frac{1 - \left(1-\frac{1}{N}\right)^N}{\left(1-\frac{1}{N}\right)^{N}}\right\} + 1 \\ \\ &= \left(1-\frac{1}{N}\right) \left[\left(1-\frac{1}{N}\right)^{-N} + N\left(1 - \left(1-\frac{1}{N}\right)^{-1} \right) - 1\right] + \frac{\left(1-\frac{1}{N}\right)^{-N}}{N} - \frac{1}{N} + 1 \\ \\ &= \left(1-\frac{1}{N}\right) \left[\left(1-\frac{1}{N}\right)^{-N} -\frac{N}{N-1} - 1\right] + \frac{\left(1-\frac{1}{N}\right)^{-N}}{N} - \frac{1}{N} + 1 \\ \\ &= \left(1-\frac{1}{N}\right)^{1-N} - 1 - 1 + \frac{1}{N} + \frac{\left(1-\frac{1}{N}\right)^{-N}}{N} - \frac{1}{N} + 1 \\ \\ &= \boxed{\left(1-\frac{1}{N}\right)^{1-N} + \frac{\left(1-\frac{1}{N}\right)^{-N}}{N} - 1} \\ \\ \end{align}

Now we can evaluate \(\lim\limits_{N \to \infty} g(N)\) term by term:

\begin{align} & \lim\limits_{N \to \infty} g(N) \\ \\ &= \left(1-\frac{1}{N}\right)^{1-N} + \frac{\left(1-\frac{1}{N}\right)^{-N}}{N} - 1 \\ \\ &= \lim\limits_{N \to \infty} \left(1-\frac{1}{N}\right)^{1-N} + \lim\limits_{N \to \infty} \frac{\left(1-\frac{1}{N}\right)^{-N}}{N} - \lim\limits_{N \to \infty} 1 \\ \\ &= e + 0 - 1 \\ \\ &= \boxed{e - 1} \\ \\ \end{align}

Therefore, the limit indeed converges to \(e - 1\), or about 1.7183. Therefore, even though the number of verses increases, if the probability of forgetting is inversely proportional to \(N\), you would on average be singing just short of twice the minimum required verses. Just be sure to drink water!