



February 4, 2022
The original puzzle can be found here.
11 polarizers preserving 80% of the original light in the end
Explanation:
We cannot turn a vertically-polarized light into a horizontally-polarized one with a perfectly horizonal polarizer because the former light contains no horizontal components. In vector algebra, we call the two lights (or vectors) orthogonal with respect to each other.
However, as the original puzzle explained, we can obtain horizontal light via two polarizers, with one at an oblique angle with respect to the vertical light. The job of the first polarizer is to filter thorough a light with some horizontal component, such that the second, perfectly horizontal polarizer would then extract that horizontal component as the output light, perfectly horizontally-polarized. The image below shows some math in its innerworkings.
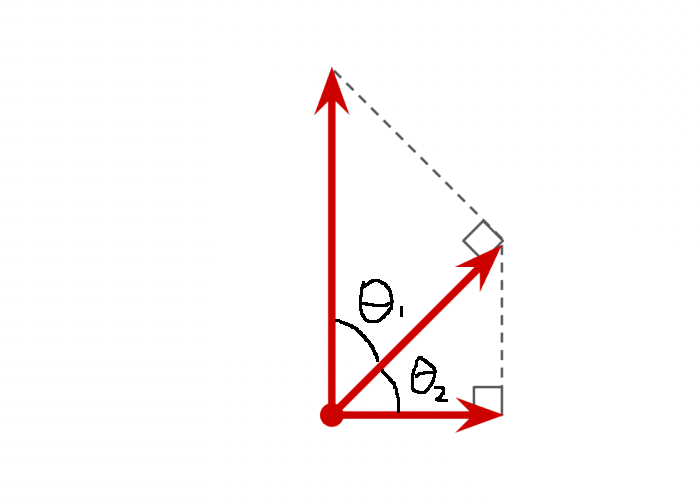
For the first polarizer at an angle \(\theta_1\) with respect to the original vertical light, the component that is filtered is \(\cos(\theta_1)\). The second horizonal polarizer then processes the horizonal component of that light, which amounts to \(\cos(\theta_2)\) of the output of the previous polarizer. In all, this means the second polarizer has output \(\cos(\theta_1) \cos(\theta_2)\) of the light from its original vertical version.
Realizing that \(\theta_1 + \theta_2 = \frac{\pi}{2}\) as the two angles must add up to 90 degrees, which is the angle between the vertical light and its horizontal counterpart, we can actually let \(\theta = \theta_1\) and therefore \(\theta_2 = \frac{\pi}{2} - \theta\) to optimize for \(\theta\) in the following optimization program:
\begin{align} \max_{\theta} &\quad \cos(\theta) \cos\left(\frac{\pi}{2} - \theta\right) \\ \text{s.t.} &\quad 0 \leq \theta \leq \frac{\pi}{2} \end{align}
The solution can be arrived as below:
\begin{align} &\max_{\theta}\left[\cos(\theta) \cos\left(\frac{\pi}{2} - \theta\right)\right] \\ &= \max_{\theta}\left[\cos(\theta) \sin\left(\theta\right)\right] \\ &= \max_{\theta}\left[\frac{\sin{\left(2\theta\right)}}{2}\right] \\ &= \boxed{\frac{1}{2}} \quad \text{achieved when} \quad \theta = \frac{\pi}{4} \\ \end{align}
Thanks to useful trig identities.
If we add the reflective factor of the polarizers, this means that we can at best receive \(\frac{(0.99)^2}{2} = 0.49\) or 49% of the original light, via the following configuration:
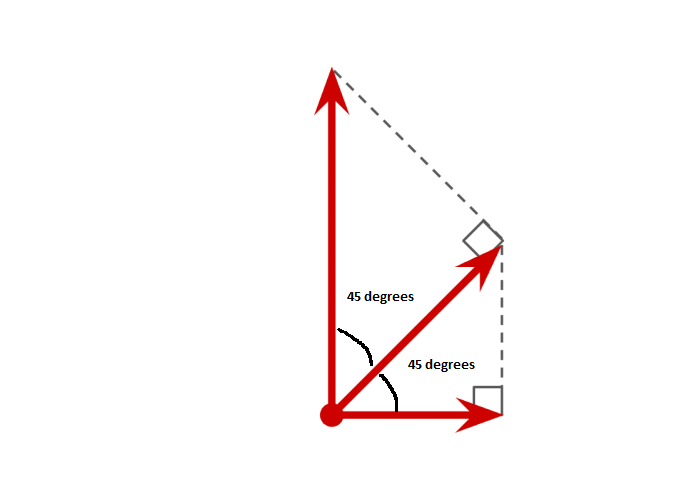
Before moving on, I want to remark on the intuitive explanation on why the first polarizer should bisect the angle between the original vertical light and its eventual horizontal counterpart:
If the first angle is too small, then the obliqued light would have too little horizonal component for the second, horizonal polarizer to extract. On the other hand, if the first angle is too large, then the obliqued light would have too little intensity for the second polarizer to process. The perfect balance occurs when the first angle bisects the angle between the vertical and the horizonal light, i.e. at 45 degrees.
Now, the puzzle is given that we would have as many polarizers as we need, so long as we output the maximum amount of light in the end. Without the fact that the polarizers reflect light, the optimal solution is to use an infinite number of polarizers, each with an angle incrementally greater than 0 with respect to the previous light. This ensures minimal loss of light through each stage while slowly generating and extracting horizonal components until the end.
However, this is clearly not the solution here, as with each added polarizer, more and more light are reflected away. This means that we have a tradeoff, as described below.
If we have too few polarizers, we would not be preserving the ideal amount of horizontal component for our horizontally-polarized light in the end. However, if we have too many polarizers, we would be reflecting too much light to have any left in the end.
In order to examine the above tradeoff mathematically, let us introduce some annotations. Let \(a\) be the attentuating factor for each polarizer. For example, as in the puzzle, if each polarizer reflect 1% of the light, then \(a = 0.99\). Let \(N = 2, 3, 4, \dots\) be the number of polarizers used, including the last, horizontal one. Finally, let \(\theta_k\), for \(k = 1, 2, 3, \dots, N\) be the angle between the kth polarizer and the previous light (if \(k = 1\) then the previous light is the original vertical one). If we fix \(a\) and \(N\), we obtain the following optimization problem in terms of \(\theta_k\)'s:
\begin{align} \max_{\theta_k} &\quad \cos(\theta_1)\cos(\theta_2)\cos(\theta_3)\dots\cos(\theta_k)\dots\cos(\theta_N)\\ \text{s.t.} &\quad \theta_k \ge 0 \quad \forall k \\ &\quad \sum_{k = 1}^N \theta_k = \frac{\pi}{2} \\ \end{align}
Even though the above optimization problem is not convex, we can still examine its KKT conditions to obtain a necessary condition for optimality. Sparing the details, an important realization is that all the angles must be equal to each other. Combined with the equality constraint, this means that: \(\theta_k = \theta = \frac{\pi}{2N}\).
Hence, we now obtain one equation representing the amount of light received in the end:
\begin{align} \text{Light Received} = \left[a \cos{\left(\frac{\pi}{2N}\right)}\right]^N \end{align}
Where \(0 < a < 1\).
We can plot the amount of light received as a function of \(N\), the number of polarizers used, while fixing \(a = 0.99\). Doing so gives the following graph:
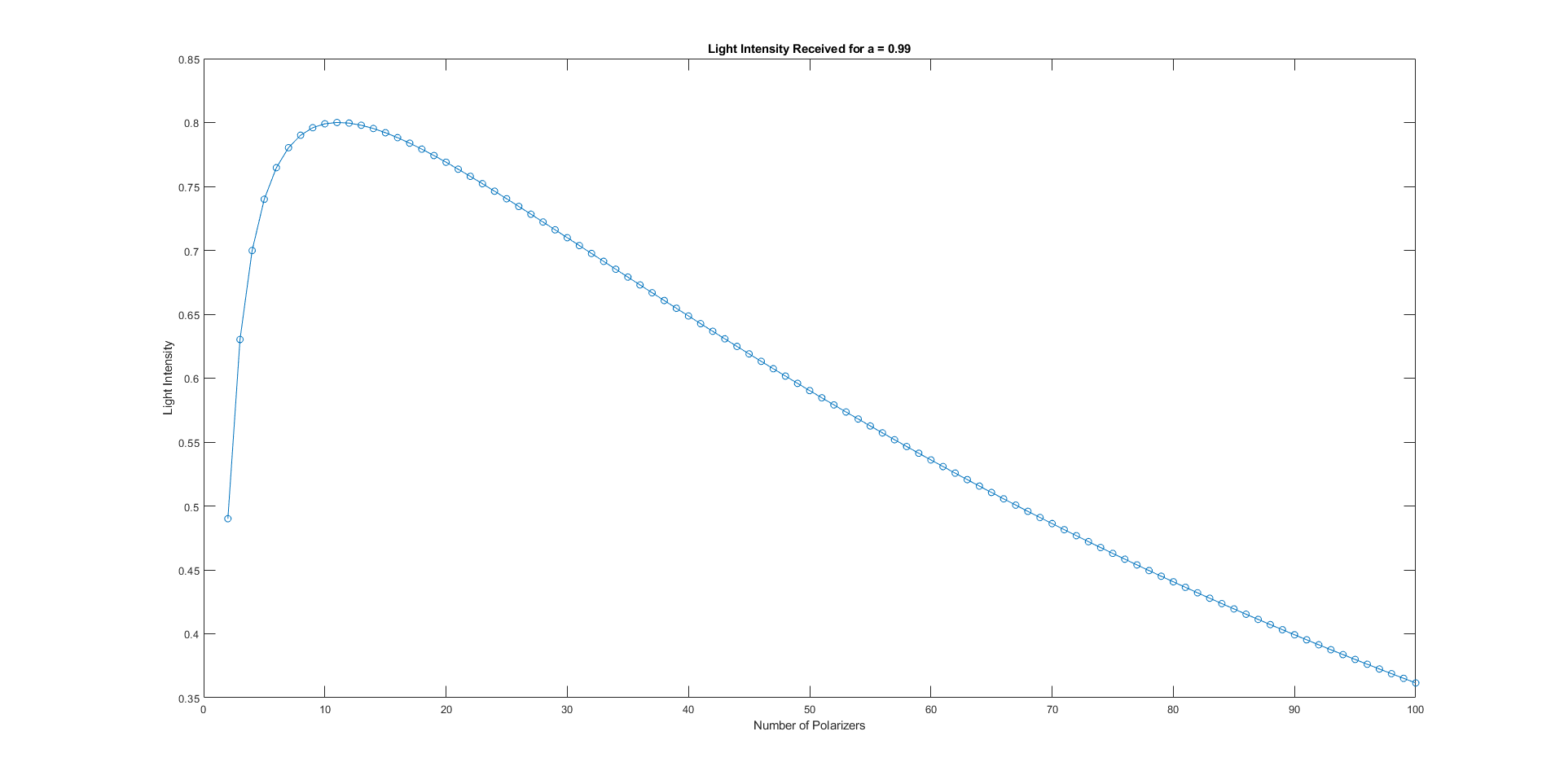
From the above graph, it is clear that for \(a = 0.99\) using 11 polarizers, each \(\frac{\pi}{22}\) or about 8.2 degrees apart, would yield the maximum intensity in the end at 0.8, or roughly 80% of the original light is preserved and now perfectly horizontally-polarized!
As we change the attentuation factor, perhaps by varying the quality of the polarizers used, we obtain different optimal points for \(N\), as the graph below illustrates:
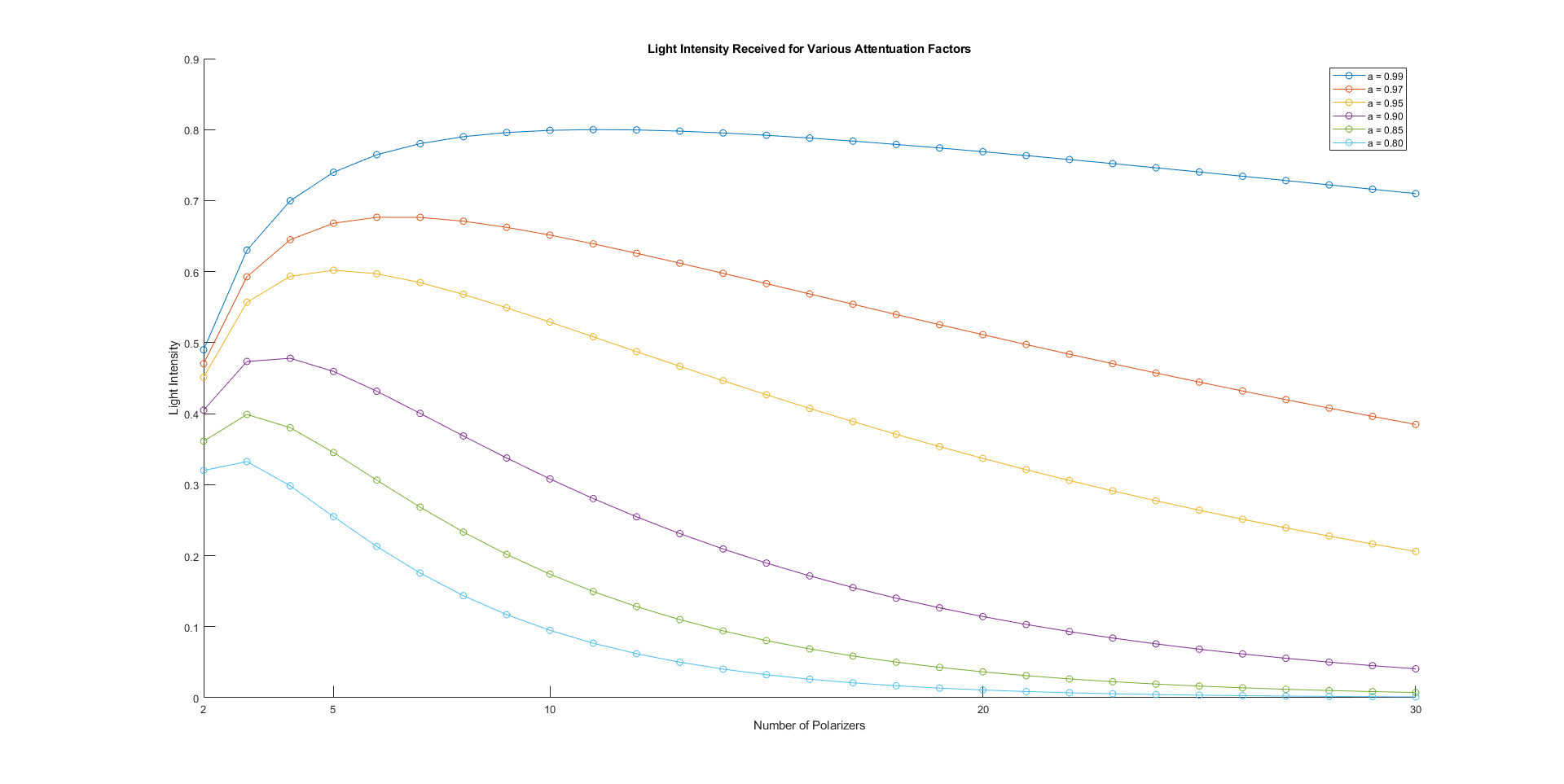
The table below summarizes the graph for various attentuation factors (bold indicates the one used for the puzzle).
| % of light reflected by each polarizer | Attentuation Factor \(a\) | Optimal Number of Polarizers \(N\) | Maximum % of Light Transmitted |
|---|---|---|---|
| 1 | 0.99 | 11 | 80 |
| 3 | 0.97 | 6 | 67.65 |
| 5 | 0.95 | 5 | 60.2 |
| 10 | 0.90 | 4 | 47.8 |
| 15 | 0.85 | 3 | 39.9 |
| 20 | 0.80 | 3 | 33.3 |
An interesting observation from the above graph is that as the polarizers start to reflect more and more light, the tradeoff quickly favors using fewer polarizers. This can be seen where even if the polarizers only reflect 15% of the light (\(a = 0.85\)), the optimal number of polarizers already drops to 3, one more than the minimum required.