



March 25, 2022
The astronomers of Planet Xiddler are back at it. They have developed a new technology for measuring the radius of a planet by analyzing its cross sections.
And so, they launch a satellite to study a newly discovered, spherical planet. The satellite sends back data about three parallel, equally spaced circular cross sections which have radii A, B and C megameters, with 0 < A < B < C. Based on these values, the scientists calculate the radius of the planet is R megameters. To their astonishment, they find that A, B, C and R are all whole numbers!
What is the smallest possible radius of the newly discovered planet?
For non-integer spacing: 8 megameters
For integer spacing: 65 megameters
Explanation:
It all comes down to the following diagram:
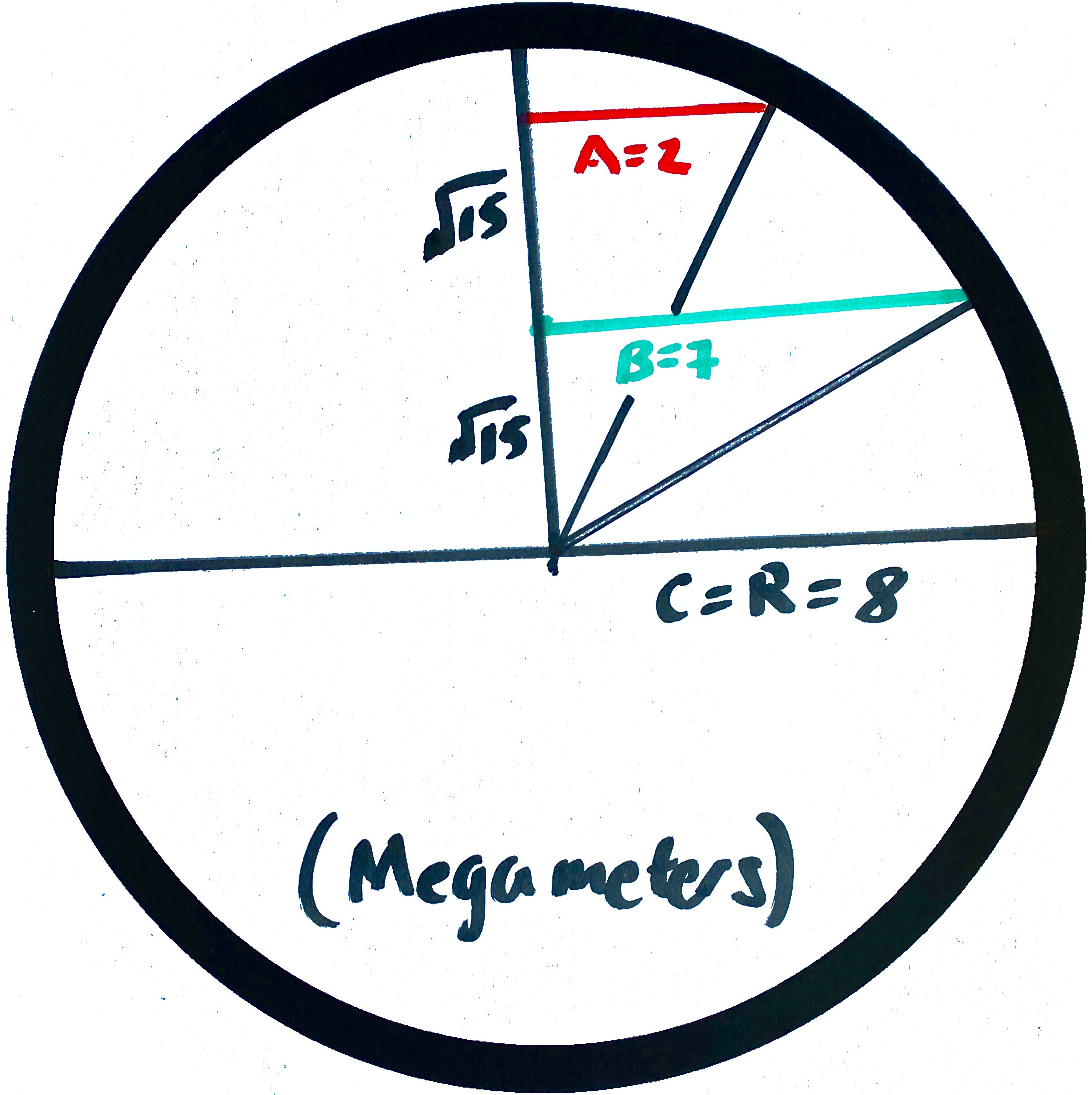
From the above diagram, the circle represents one of the great circles of Xiddler, the largest possible cross-section of the spherical planet. Hence, the center of the circle is also that of the planet. The radius of the great circle, R, is the same as that of the planet as well. Without loss of generality, let the above diagram be the side view of the cross-sections taken by the satellite. Hence, each of the cross-sections A, B, and C, are horiontal lines. Cross-sectional radii A, B, and C, together with the spherical radii that is perpendicular to them, form three right-angled triangles with hypotenuse R.
For the smallest R, it makes sense for it to overlap with C, the longest radius of the three for the cross-sections. We must have R at least 3 as A is at least 1 and B is at least 2. From then on, realizing that the distance between B and C, call it \(d_2\), must be half of that for A to C, call it \(d_1\), we have the following relation:
\begin{align} d_1 &= 2d_2 \\ d_1^2 &= 4d_2^2 \\ \end{align}
With \(d_1^2\) and \(d_2^2\) integers. That means we can iterate through all possible values of R to find the smallest possible one that satisifies the \(d_1^2 = 4d_2^2\) constraint. This can be done via MATLAB:
found = false;
for R = 3:100
for A = 1:R
d1Squared = R^2 - A^2;
if mod(d1Squared, 4) ~= 0
% d1^2 is not divisible by four, not a solution
continue;
end
d2Squared = d1Squared / 4;
B = sqrt(R^2 - d2Squared);
% Check if B is an integer
Z = ceil(B);
if Z == B && Z > A
found = true;
break;
end
end
if found
break;
end
end
% Output:
A =
2
B =
7
R =
8
Therefore, it follows that the smallest R that satisfies the requirement is \(R = 8\), with
And the distance between cross-sectional planes being \(\sqrt{15}\). All units are in megameters. This is illustrated in the diagram above.
If we want to find the smallest radius when the distances between the cross-sections are integers, then we must peer into the world of Pythagorean triples.
Now, we are given that A, B, C, and R are all positive integers. This means we are on the hunt for Pythagorean triples. We need to find a number for R that represents the hypotenuse for three distinct right-angled triangles. This seems like a tall order, until we make use of primitive Pythagorean triples. A primitive Pythagorean triple \((a, b, c)\) is one such that the greatest common divisor (gcd) among the three elements is 1. This is significant as once we obtain such triplets, \((a, b, c)\), we can generate infinite triplets by scaling the primitive one by an integer factor, \(k\), to obtain \((ka, kb, kc)\).
Our strategy for the hunt of a hypotenuse that can be part of at least three distinct triples is therefore as follows:
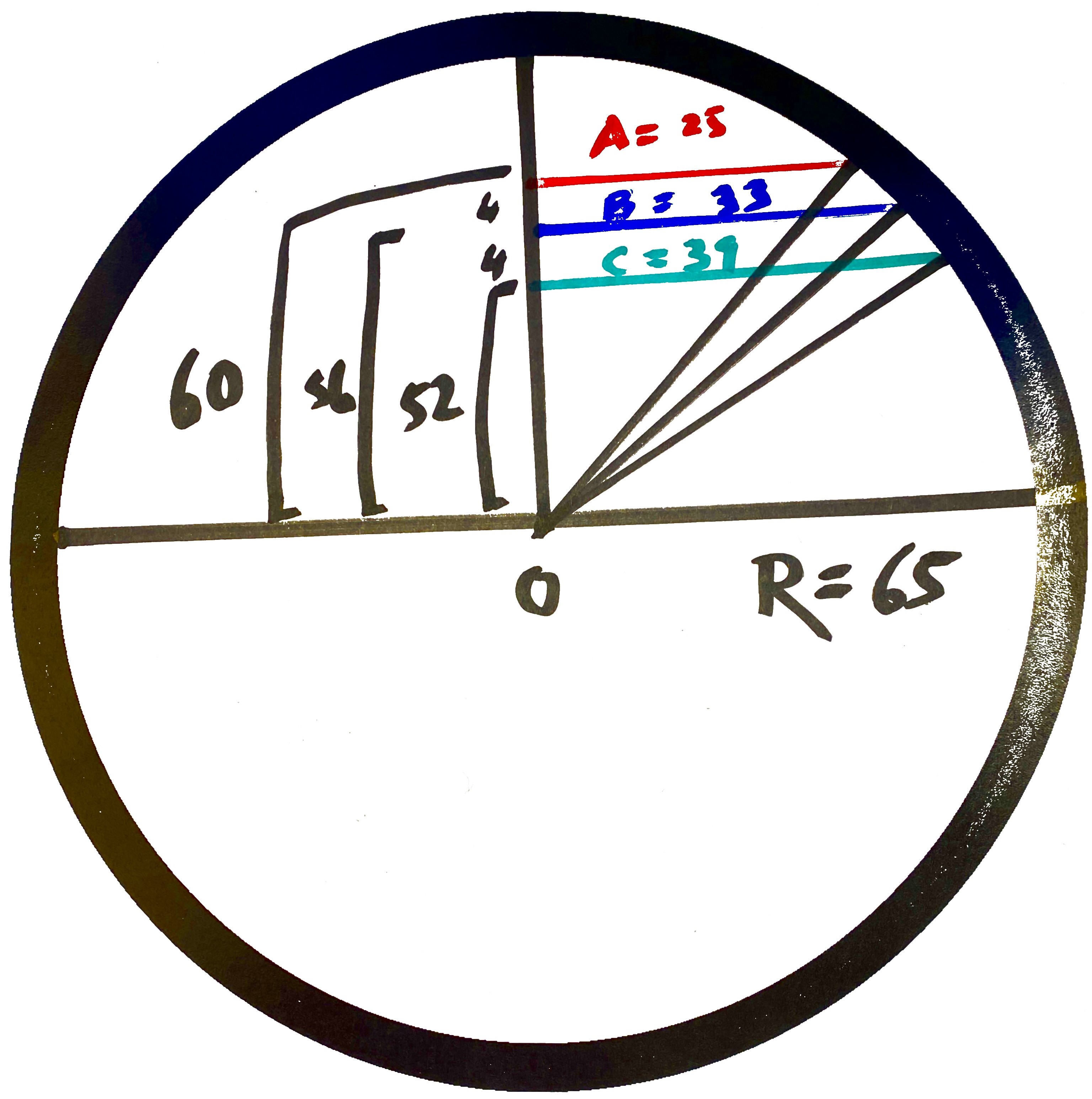
The two smallest values that can act as hypotenuses of primitive Pythagorean triples are 5, and 13, with their respective triples being \((3, 4, 5)\) and \((5, 12, 13)\). The lcm of 5 and 13 is their product, 65, as the two values are co-prime. It turns out that 65 is also a hypotenuse for a primitive Pythagorean triple: \((33, 56, 65)\). Therefore, let's cross our fingers and hope that the final constraint of the planes being evenly-spaced would be satisfied with \(R = 65\).
First, scaling \((3, 4, 5)\) by factor of 13 yields \((39, 52, 65)\).
Next, scaling \((5, 12, 13)\) by factor of 5 yields \((25, 60, 65)\).
Finally, let's bring back 65's own primitive triple: \((33, 56, 65)\). Notice in all three cases, the middle element, i.e. the long leg of the right-angled triangle, form an arithmetic sequence: \(\{52, 56, 60\}\). Therefore, by making the short legs to be the radii of the cross-sections, and arranging them such that 0 < A < B < C as stated in the problem, we obtain:
As shown in the diagram. Units are in megameters. The planes are evenly-spaced 4 megameters apart. This verifies that \(R = 65\) megameters is the smallest R that satisfies all the requirements in the puzzle if the spacing is an integer.