



July 1, 2022
As the Royal Astronomer of Planet Xiddler, you wake up from a dream in which you measured the planet’s radius using a satellite. “How silly!” you think to yourself. “Satellites haven’t even been invented yet!” And so you and another astronomer set out to investigate the curvature of the planet.
The two of you climb two of the tallest towers on the planet, which happen to be in neighboring cities. You both travel 100 meters up each tower on a clear day. Due to the curvature of the planet, you can barely make each other out.
Next, your friend returns to the ground floor of their tower. How high up your tower must you be so that you can just barely make out your friend again?
About 300m for a "planet-sized" planet.
Explanation:
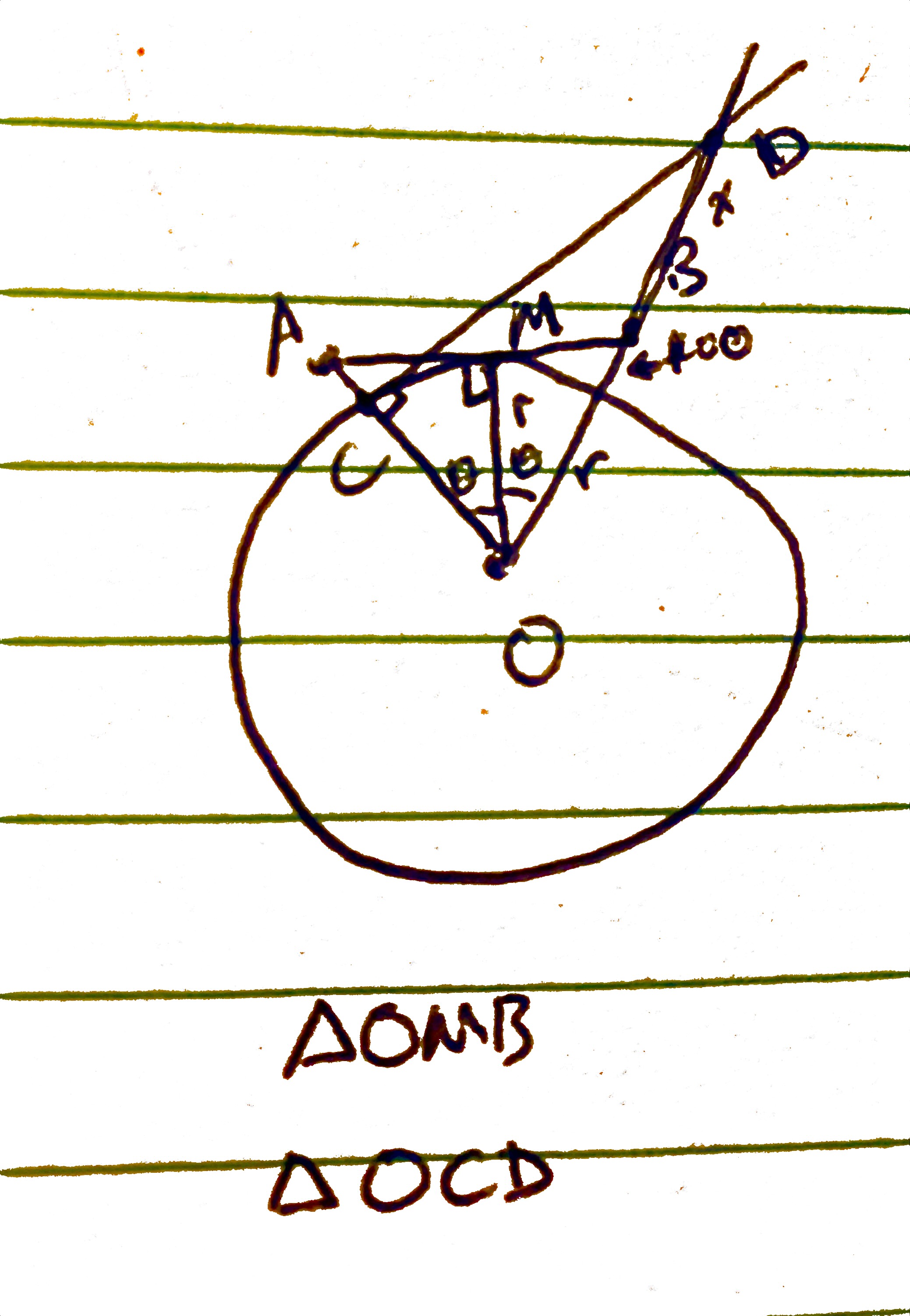
Everything you need to know about this Xiddler's towering experiment is described in the miniature diagram below:
We are making several assumptions here:
With those assumptions, the diagram above depicts a cross-section of the planet Xiddler, which is a circle. Let \(O\) be the center of the circle, and \(r\) be Xiddler's radius. Let B be your location as you climbs 100m above your tower, to which your friend does the same, at A. Let C be the point where your friend descends back down to the planet's surface.
The first triangle to note is \(\Delta OMB\), which is simply half of \(\Delta OAB\). This allows a point \(M\) on the circle such that \(OM\) is both the median and the altitude of \(\Delta OAB\), made possible by the given fact that at 100m, both you and your friend barely makes out each other. The line-of-sightwould be \(AB\), through \(M\). Therefore, \(\Delta OMB\) is a right-angled triangle with \(OM = r\) and \(OB = r + 100\).
Letting \(\angle MOB = \theta\), we therefore have:
\begin{align} \cos \theta &= \frac{r}{r+100} \\ \end{align}
And the same for \(\angle MOA\).
The second triangle of note is \(\Delta OCD\). This is created when your friend comes down from their tower. At \(C\), where your friend lands, the line-of-sightbetween you and your friend goes through the planet, and therefore you no longer see them unless you extend \(OB\) to \(D\), where you would barely make out your friend with the line-of-sight\(CD\). Since at \(D\) is where you first see your friend, \(CD\) is tangent to the circle. Here is the figure from above again for your convenience:

Therefore, we have another right-angled triangle in \(\Delta OCD\). Since \(\angle MOB = \angle MOA\ = \theta\) and \(\angle AOB = \angle MOB + \angle MOA\), we have \(\angle AOB = 2\theta\). Since \(OB\) is extended to \(D\) and \(OC\) is extended to \(A\), we have \(\angle COD = 2\theta\). We let \(BD = x\). Hence, applying definition of cosine once again:
\begin{align} \cos 2\theta &= \frac{r}{r+100 + x} \\ \end{align}
Using the double angle formula for cosine, which is:
\begin{align} \cos^2 \theta &= \frac{1 + \cos 2\theta}{2} \\ \end{align}
We have:
\begin{align} \left(\frac{r}{r+100}\right)^2 &= \frac{1}{2} \left(\frac{r}{r+100+x}\right)\\ \end{align}
Please note that the answer we are looking for is in \(x\). Although \(r\) is a variable, we can let it go to infinity since it is much larger than the scale of the constant figures in this problem, such as the distance of the two cities and the climbed length of the tower, which is a mere 100m. Therefore, we will first solve \(x\) in terms of \(r\) and then look for patterns there.
Solving for \(x\):
\begin{align} x &= \frac{100(3r^2 + 400r + 10000)}{r^2 - 200r - 10000} \\ \end{align}
Of course, as \(r >> 100\), we do not have to worry about the denominator being 0 or negative. Now that we have a function of \(x\), what does it look like graphically?
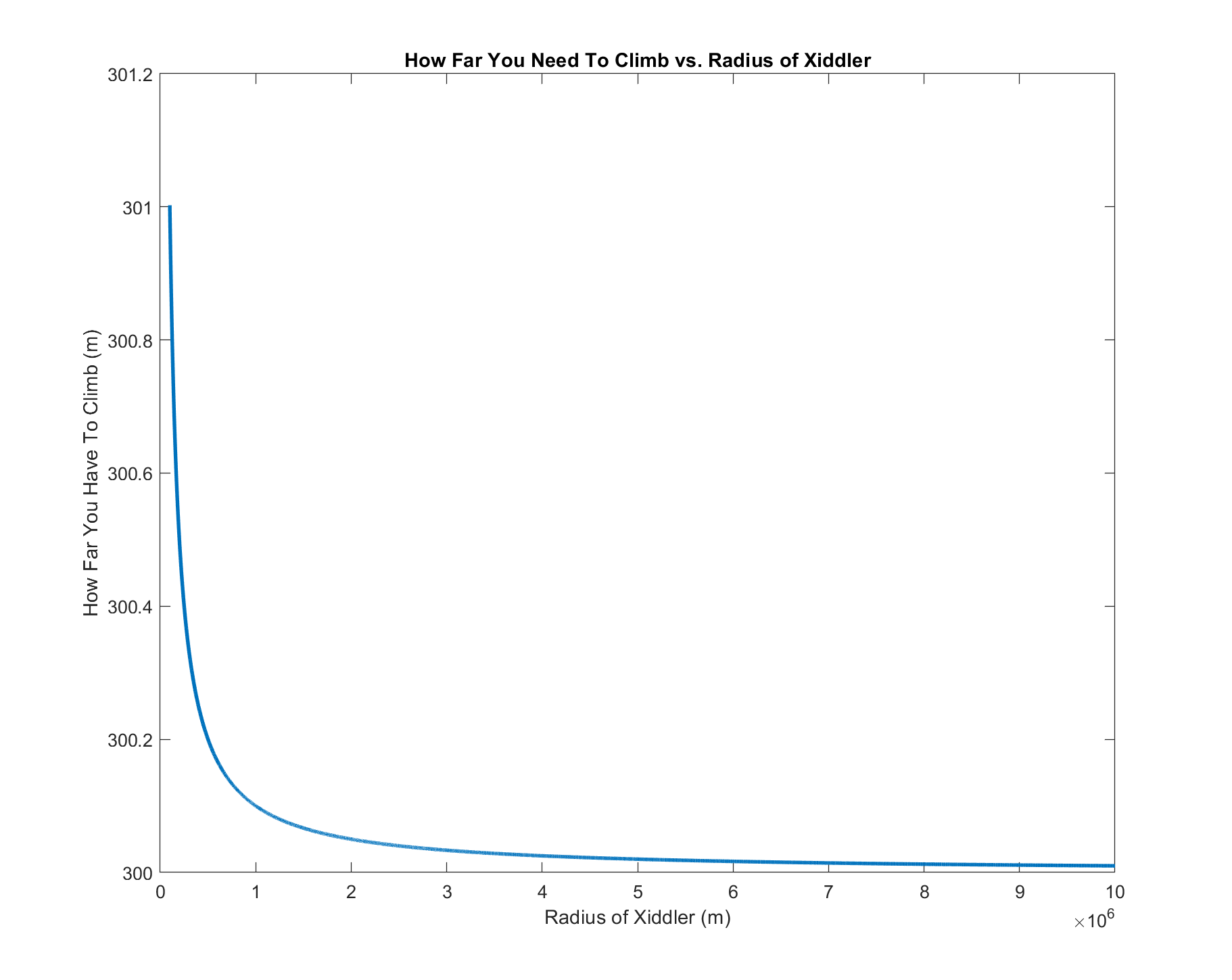
You can see that how far you have to climb quickly converges to 300m as the radius of the planet increases. In fact, the convergence is so drastic that even at 100km as the radius of the planet, which is not even big enough to make that planet a sphere in reality, you would only need to climb 1m more than had the planet's radius been 10000km, which is bigger than that of the Earth. If Xiddler had the same radius as that of the Earth at 6371km, the value of \(x = 300.016\)m, which is only 1.6cm more than the converging value had the radius been infinite.
Evaluating the limit confirms the convergence:
\begin{align} &\lim_{r \to \infty} \frac{100(3r^2 + 400r + 10000)}{r^2 - 200r - 10000} \\ &= \frac{100(3r^2)}{r^2} \\ &= \boxed{300} \\ \end{align}
In the original problem, the intention of the experiment was to measure the radius of Xiddler. While it is possible to do so from the given setup, we have seen that it is extremely sensitive to small variations in a large \(r\). In reality, you would always be climbing about 300m more than the original 100m climb after your friend has come down, as we've seen in the convergence of the expression for \(x\). If we factor in the simplifying assumptions, such as height of the astronomers and any imperfections of the spherical shape of Xiddler caused by, say, its rotation, then this experiment would be impractical in measuring the radius of the planet given the small margin of error and the sensitivity of the dependent variable.