



July 16, 2021
Italy defeated England in a heartbreaking (for England) European Championship that came down to a penalty shootout. In a shootout, teams alternate taking shots over the course of five rounds. If, at any point, a team is guaranteed to have outscored its opponent after five rounds, the shootout ends prematurely, even if each side has not yet taken five shots. If teams are tied after five rounds, they continue one round at a time until one team scores and another misses.
If each player has a 70 percent chance of making any given penalty shot, then how many total shots will be taken on average?
Approximately 10.78 kicks on average.
Explanation:
This puzzle can easily be simulated via Monte Carlo to obtain a decent approximation to the expected number of kicks in a penalty shootout. Below is a graph of the Monte Carlo simulations against various conversion rates, denoted in this write-up as \(c\). In the problem, \(c = 0.7\).
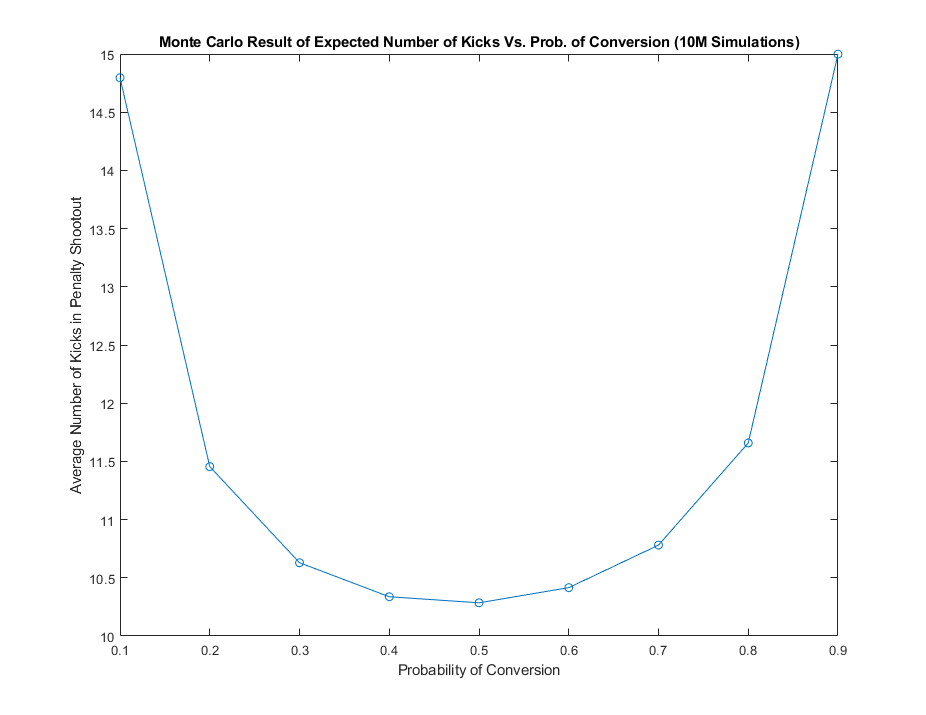
In particular, when \(c = 0.7\), the expected number of kicks comes to be approximately 10.78.
The above chart is convex and (roughly) symmetric about \(c = 0.5\). The symmetry is expected because a miss in a penalty is as good as a score when both sides have the same probability of conversion. The convexity is also expected. Imagine if both side's goalkeepers are talented enough to keep \(c\) at a very low value, such as \(c = 0.1\). This means with a high probability, both sides will end the regulation in a 0-0 tie and head to overtime, where more kicks will be needed to decide the winner. As \(c\) converges to 0.5, more variabilities are introduced and it becomes more and more likely that after 10 or fewer kicks, we will have an uneven score leading to fewer kicks needed to decide the winner.
It is possible to obtain the theoretical answer. One way is to use Markov Chains to track the state of the penalty shootout as the current scores of each team after the most recent kick as well as the number of kicks already executed. The transition probabilities would either be \(c\) if the most recent kick is a conversion or \((1-c)\) for a miss. In either case, the kick counter increments by one and the score updates accordingly. A terminal state would either consists of an uneven score where the winner emerges after the losing side runs out of possible kicks to catch up, or with 10 kicks and the score is tied and the shootout reaches overtime. The overtime state is still a terminal state because no Markov Chains are needed in the ensuing analysis, as seen below:
Let's first pull out some tools useful for solving the puzzle in the overtime case. The first utility is geometric distribution. If \(X\) is a (discrete) random variable distributed geometrically, then it represents the number of trials when the first success is reached. Here we assume each trial is independent and identically distributed with the Bernoulli variable \(p\). Therefore, \(X\) would have the Probability Mass Function (pmf) \(P(X = k) = p(1-p)^{k-1}\). More importantly though (and something you can try to show), the average value of \(X\) would simply be \(\frac{1}{p}\).
Why is the above tool useful in our case? In our problem, if the penalty kick goes into overtime, meaning each team had five kicks and the score is tied, then the "extra" pair of kicks each would consist of a trial. Assuming each player's conversion rate is independent of others, the probability of "success", i.e. the penalty kicks ending on a particular pair of kickers, would be: \(2c(1-c)\), since we need to have one kicker miss while the other scores, and there are two possible scenarios. Let us denote \(p = 2c(1-c)\). Therefore, the pair of kickers in each round of extra time would consist of a trial. If \(X\) denotes the number of trials before we settle the score (no pun intended), then \(X\) is distributed geometrically with probability of success \(p\), and the expected rounds in extra time would be \(\frac{1}{p}\). The expected number of extra kicks would then be \(\frac{2}{p} = \frac{2}{2c(1-c)} = \frac{1}{c(1-c)}\), since there are two kicks in each round in extra time.
It is interesting to see that \(c(1-c)\) is maximized when \(c = 0.5\), meaning \(\frac{1}{c(1-c)}\) would be minimized in this case. This reinforces the intuition that the expected number of kicks would be mimized if \(c\) approaches 0.5 from both the 0 and the 1-end.
Markov Chains applied to analyze the expected kicks using the current scores and the number of kicks as states would allow for the determination of the following parameter: \(p_c(n)\). This is the probability that the penalty shootout would end in \(n\) kicks with the probability of conversion \(c\) in regulation. Clearly, by inspection, the possible values of n are 6, 7, 8, 9, and 10. Furthermore, we can denote \(p_c = \sum_{n=6}^{10} p_c(n)\) as the probability that the penalty shootout would be determined in regulation. Putting everything togehter, we can obtain an expression for the theoretical answer as given below.
\begin{align} &\text{Expected Number of Kicks}\\ &= \left(\sum_{n=6}^{10} n p_c(n) \right) + \left(1 - p_c \right)\left(10 + \frac{1}{c(1-c)}\right) \\ \end{align}
Where the "10" in the second term comes from the fact that by the time overtime is reached, we would already had 10 kicks in total during regulation.
If anyone used Markov Chain approach and comes up with the state diagram, please feel free to show me!