August 16, 2021
From Oliver Ruebenacker comes a “classic” indeed:
You have four standard dice, and your goal is simple: Maximize the sum of your rolls. So you roll all four dice at once, hoping to achieve a high score. But wait, there’s more! If you’re not happy with your roll, you can choose to reroll zero, one, two or three of the dice. In other words, you must “freeze” one or more dice and set them aside, never to be rerolled. You repeat this process with the remaining dice — you roll them all and then freeze at least one. You repeat this process until all the dice are frozen. If you play strategically, what score can you expect to achieve on average?
Extra credit: Instead of four dice, what if you start with five dice? What if you start with six dice? What if you start with N dice?
Approximately 18.77 for four dice; For large \(N\), the expected high score can be approximated as \(\boxed{S = 6N - 6.75}\).
Strategy: for all dice that can be re-rolled, re-roll those that are not 6 unless 3 chances left. For 3 or 2 chances, threshold becomes 5. For one more roll left, threshold becomes 4.
Explanation:
Ususally with problems like this, I like to start simple and consider, say, the two dice scenario. However, in this puzzle, it would actually be helpful to think the other way around. What if you played this game with one million dice? Suffice to say, on your first roll, the probability of NOT rolling at least one "6" among one million rolls is...well, 0. It's actually \(1 - \left(\frac{5}{6}\right)^{1000000}\), which is essentially 0. This leads to an important observation. Even though getting a "6" on a roll is not very likely, the chance of getting at least one "6" after multiple tries increases rapidly. And one "6" is all we need.
Continuing with our "one million dice" scenario, the maximum possible score we can obtain is 6 million. Due to the sheer number of dice involved, our expected high score using the strategy of "Get a 6 or bust" actually gives us pretty darn close to 6 million. Monte-Carlo simulations routinely provided values of above 5,999,990, which is within 0.001% of the theoretical maximum.
...Except we don't have that many dice. In fact, for the original problem, we only have four. That's okay. Assuming a fair die rolled \(n\) times, the probability of getting at least a "\(k\)" once in those \(n\) rolls is \(1 - \left(\frac{k-1}{6}\right)^{n}\) which gets very close to 1 for \(n\) not having to get very large. For example, for \(k = 5\), already \(1 - \left(\frac{5-1}{6}\right)^{2} = \frac{5}{9} > \frac{1}{2}\), and so with just two rolls, we are more likely than not to get a "5", the second highest roll. For "6", that magic roll number only goes up to 4.
Which leads us to a neat strategy: count how many times a dice will be rolled (including the current roll). If that number is 4 or greater, only settle with a "6". If the number of rolls remaining is 2 or 3, settle for 5 or greater. Only when there is one roll left (for one die), do we settle, for that die only, 4 or greater. We are then expected to lose points from the maximum score via the following cases:
We lose, then, on average 2.5 + 1.75 + 2.5 = 6.75 points from the theoretical maximum.
Theretical score: \(\boxed{S = 6N - 6.75}\) for large \(N\).
The Monte-Carlo simulation of this strategy can be programmed via MATLAB as follows:
function maxScore = playDicePoker(numDice)
% One trial of max score from dice poker
% Given the number of dice
maxScore = 0;
rolls = randi(6, [numDice, 1]);
subRolls = rolls;
freezeCount = 0;
while freezeCount < numDice
newRolls = NaN(size(subRolls));
[~, ind] = max(subRolls);
rollsRemaining = numDice - freezeCount;
threshold = findThreshold(rollsRemaining);
for k = 1:length(subRolls)
curRoll = subRolls(k);
if curRoll < threshold && k ~= ind
% The roll is below the threshold and we don't have to
% freeze this roll, re-roll the dice
% We add this current roll to the new roll to re-roll
newRolls(k) = randi(6);
else
% We freeze this roll and add the score to the maxScore we
% receive
maxScore = maxScore + curRoll;
% Update Counters
freezeCount = freezeCount + 1;
end
end
% We update the subRolls
subRolls = rmmissing(newRolls);
end
end
function threshold = findThreshold(rollsRemaining)
% Finds the threshold given rolls remaining
% Rolls remaining must be postive integer
switch rollsRemaining
case 1
threshold = 4;
case 2
threshold = 5;
case 3
threshold = 5;
otherwise
threshold = 6;
end
end
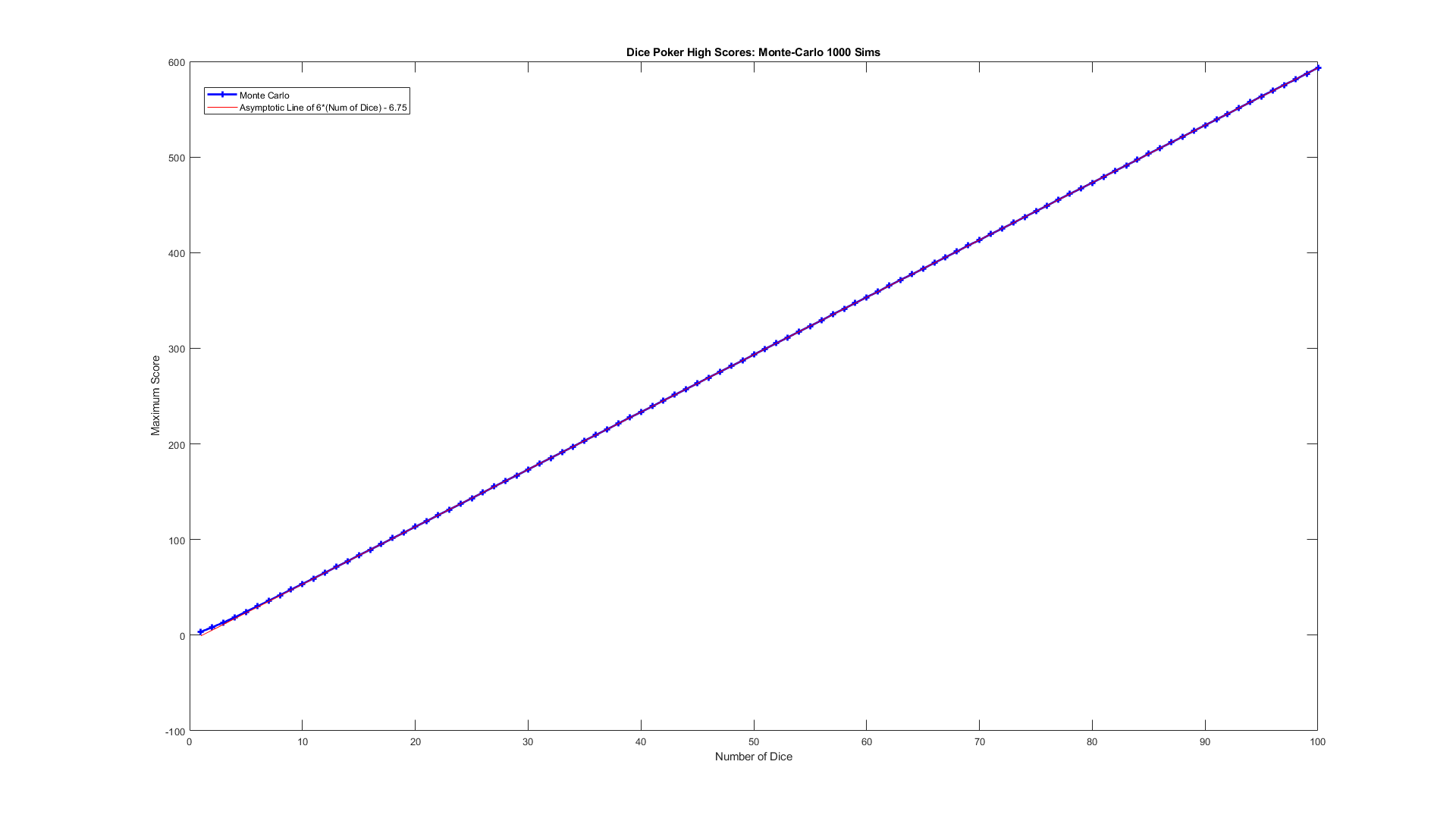
Using Monte-Carlo simulation for the above strategy, we obtain the expected high score four dice as 18.77:
Here is the Monte-Carlo of the first 100 dice's expected maximum score, with the \(\boxed{S = 6N - 6.75}\) reference line:
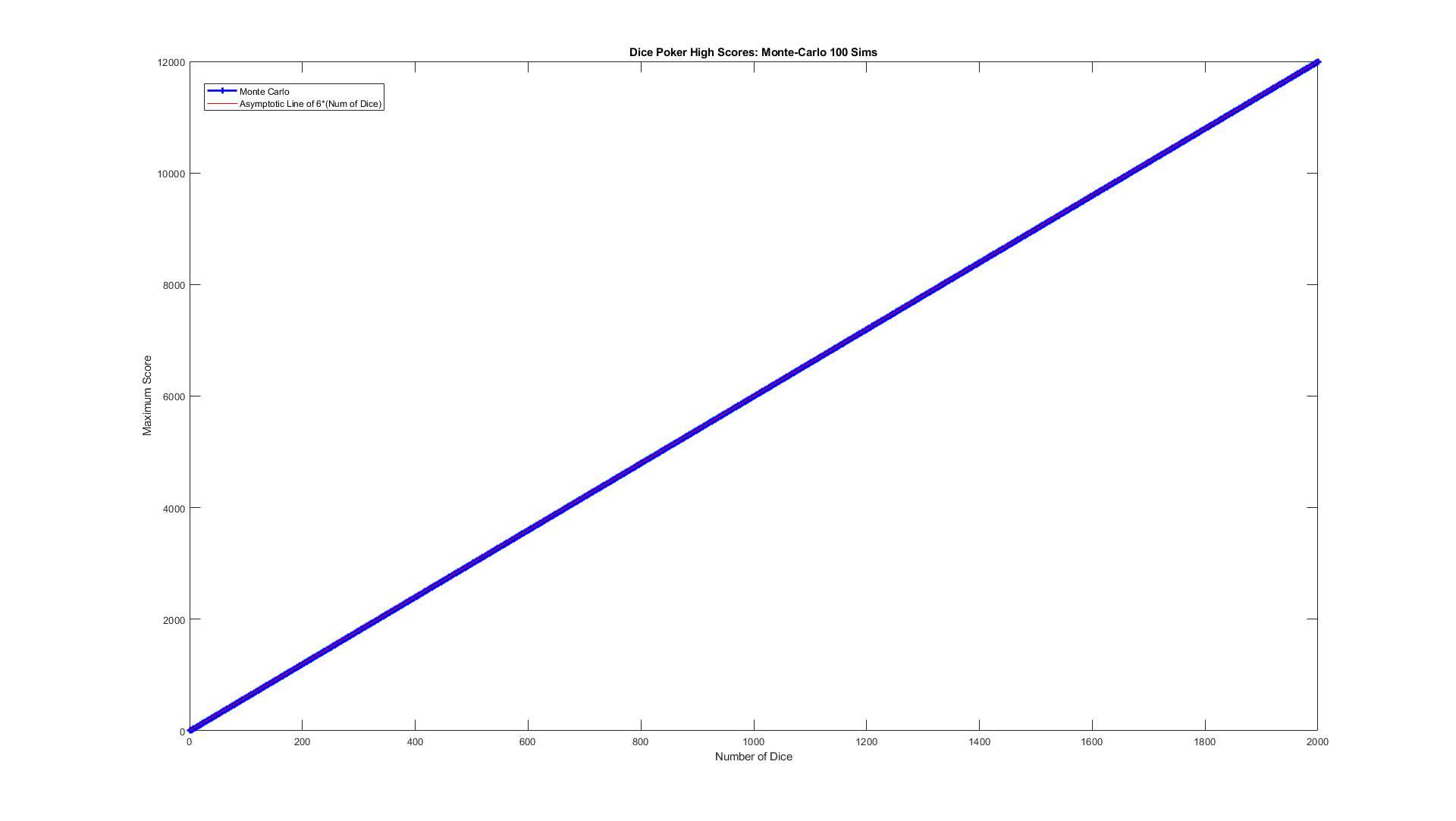
For large number of dice, it is pretty indistiguishable from the theoretical maximum as the gap is constant.