Riddler Classic: December 2, 2022

David Ding

December 2, 2022

World Cup Glory

Explanation:

Let \(M\) be the number of American fans and \(N\) be the number of Dutch fans. In the original puzzle, \(M = 11\) and \(N = 7\). Let \(P(M, N)\) represent the probability that the last shuttle ferries American fans. Here I will provide two interpretations of the puzzle, with the latter being the "official" version since it has been stated by the puzzle's author, Starvind.

The first interpretation is that the hotel rooms are randomly arranged in the beginning, and the bus driver simply calls out this random arrangement in order without the arrangement changing during the process. Then, the probability that the last shuttle ferries American fans is simply equivalent to the probability of having all of the Dutch fans occupy the first \(M + N - 1\) slots in that arrangement. That is:

\begin{align} P(M, N) &= \frac{\binom{M + N - 1}{N}}{\binom{M + N}{N}} \\ \\ &= \frac{\frac{(M + N - 1)!}{N!(M - 1)!}}{\frac{(M + N)!}{N!M!}} \\ \\ &= \frac{(M + N - 1)!M!}{(M + N)!(M - 1)!} \\ \\ &= \boxed{\frac{M}{M + N}} \\ \end{align}

So the probability that the last shuttle ferries American fans is simply the ratio of number of American fans to the total number of fans. In this case, it comes out to be \(\frac{11}{18}\).

However, the second interpretation is that the arrangement does change during the process, such as once a fan is called and cannot board the bus, the draw is randomly shuffled again. This appears to be the intent of the puzzle setup, as confirmed by the puzzle's author:

Goes back to random draw. Hence yes, there could be two consecutive Dutch shuttles.

— Arvind Hariharan (@arvindh) December 4, 2022

For all we know, the answer could still be \(\frac{11}{18}\). However, we need to take a different approach here, namely using dynamic programing. Here, we write \(P(M, N)\) a different way:

\begin{align} P(M, N) &= \sum_{k = 1}^M s_A(k, M, N)P(M - k, N) + \sum_{k = 1}^N s_D(k, M, N)P(M, N - k) \\ \end{align}

The main observation is that the probability only depends on the current distribution of fans. Once a fan is denied boarding the bus, the puzzle turns into: "what is the probability that the last shuttle ferries American fans given the remaining distribution of fans?". Those probabilities are weighted by the probabilities that the remaining distribution occurs. Here, \(s_A(k, M, N)\) is the probability that \(k\) successive Americans are called given \(M\) American fans and \(N\) Dutch fans, and \(s_D(k, M, N)\) is the Dutch counterpart. Those probabilities are given as:

\begin{align} s_A(k, M, N) &= \frac{\binom{M + N - k - 1}{N - 1}}{\binom{M + N}{N}} \\ \\ s_D(k, M, N) &= \frac{\binom{M + N - k - 1}{M - 1}}{\binom{M + N}{M}} \\ \end{align}

Let me explain \(s_A(k, M, N)\) to shed some light. The number of fan arrangements such that the bus driver calls \(k\) American fans first is the same as having the last \(M + N - k\) fans arranged in this order: Dutch, and the rest of the fans. This means we need to arrange \(N - 1\) Dutch fans among \(M + N - k - 1\), of which there are \(\binom{M + N - k - 1}{N - 1}\) ways to do it. The total number of ways to arrange all the Dutch fans is \(\binom{M + N}{N}\), hence the probability for \(s_A(k, M, N)\). Similar explanation for \(s_D(k, M, N)\).

The base cases are given as below:

\begin{align} P(0, N) &= 0 \\ P(M, 0) &= 1 \\ \end{align}

Clearly, when there are no American fans left to board, then the last shuttle necessarily takes a Dutch fan, hence the probability is 0; and vice versa.

With those base probabilities and the transition, we can code up the probability matrix as follows (here done in MATLAB):

clear;
clc;
close all;

%% Main script
global probMatrix; %#ok

M = 11;
N = 7;
probMatrix = NaN(M + 1, N + 1); % account for zero fans of a certain country (Matlab is 1-based)
prob = getProb(M + 1, N + 1);

%% The recursive function
function prob = getProb(M, N)
    global probMatrix; %#ok
    % Function to set the probability matrix
    % Note that MATLAB is 1-based

    % base cases
    if M <= 1
        % No more American fans left
        probMatrix(M, N) = 0;
        prob = 0;
        return;
    end

    if N <= 1
        % No more Dutch fans left
        probMatrix(M, N) = 1;
        prob = 1;
        return;
    end

    % offset 1-based
    Mreal = M - 1;
    Nreal = N - 1;
    totalReal = Mreal + Nreal;

    probPart1 = 0;
    for k = 1:Mreal
        probPart1 = probPart1 + (nchoosek(totalReal - k - 1, Nreal - 1)/nchoosek(totalReal, Nreal))*getProb(M - k, N);
    end

    probPart2 = 0;
    for k = 1:Nreal
        probPart2 = probPart2 + (nchoosek(totalReal - k - 1, Mreal - 1)/nchoosek(totalReal, Mreal))*getProb(M, N - k);
    end

    % Transition
    prob = probPart1 + probPart2;
    probMatrix(M, N) = prob;
end

We get the following probability matrix:

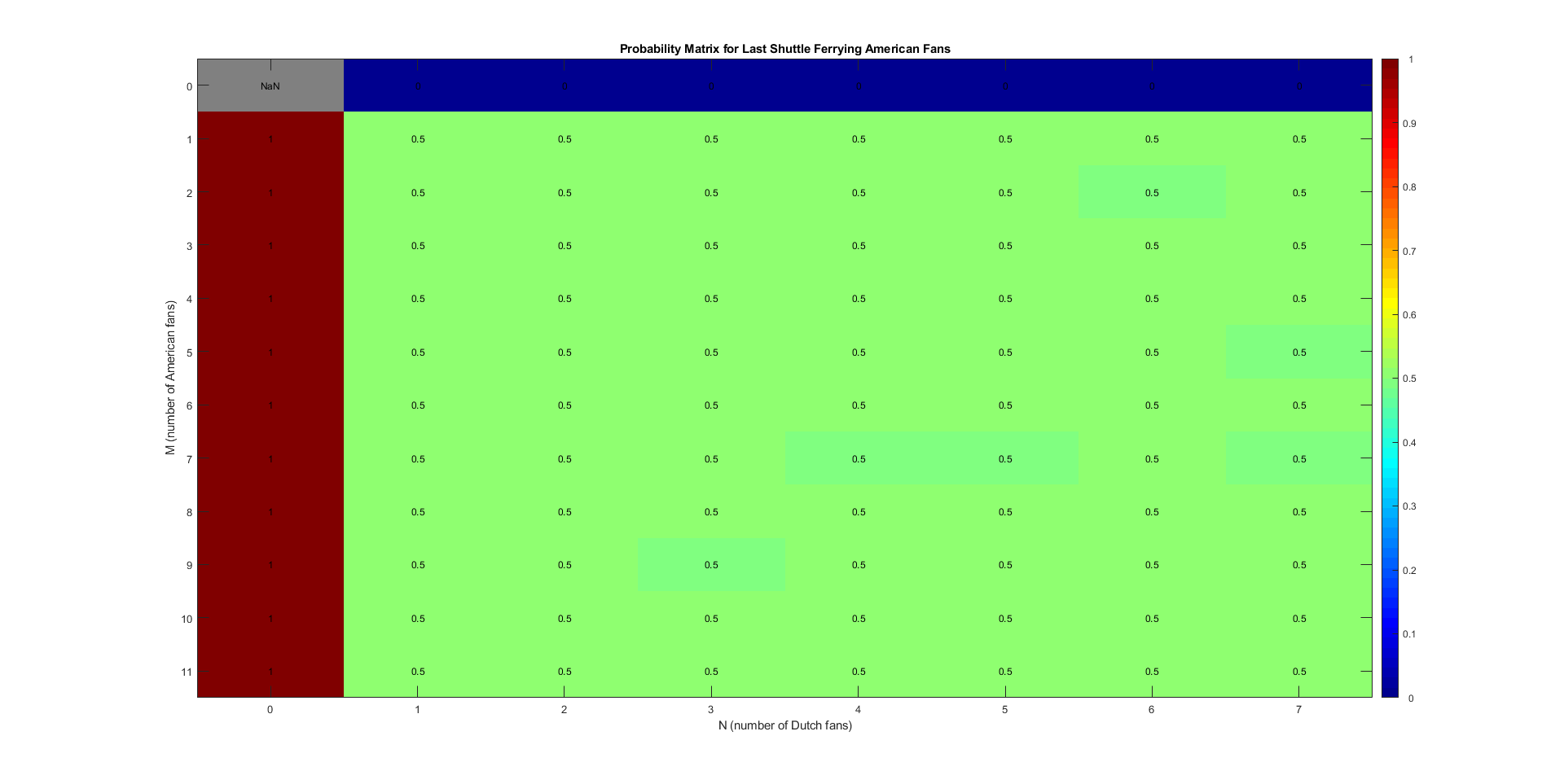
The probability that we want is \(P(M, N)\), which for the values given in the puzzle, can be found in the lower-right corner of the probability matrix:

\(P(M = 11, N = 7) = 0.5\). In fact, all but the edge cases have the probabilities at 0.5. This is similar to a chocolate-eating problem by Henk Tijms two years ago on Riddler, in which a nice proof of induction was given to show that the probabilities are in fact 0.5 except for the edge cases. However, I have another intuitive explanation to this observation. Imagine if we have 1 American fan and a million Dutch fans. As long as the Dutch fans far outnumber the lone American fan, we will get long streaks of Dutch fans boarding the bus. If the lone American fan is called, as long as he/she is not called first, the possibility is not lost as that fan just goes back to the draw, and we continue to have long streaks of Dutch fans again. So, everything balances out to be 0.5.