



March 5, 2021
You have three coins in your pocket, each of which can be a penny, nickel, dime or quarter with equal probability. You might have three different coins, three of the same coin or two coins that are the same and one that is different.
Each of these coins can buy you a string whose length in centimeters equals the value of the coin in cents, i.e., the penny buys 1 cm of string, the nickel buys 5 cm of string, etc. After purchasing your three lengths of string, what is the probability that they can be the side lengths of a triangle?
Answer: \(\frac{11}{32}\)
Explanation:
Here we are assuming that should the strings form a triangle, the triangle is one formed from a closed triangle on a 2D Euclidean plane. Simply put, the side lengths of the ensuing triangle must satisfy the triangle inequality. This is illustrated as below:
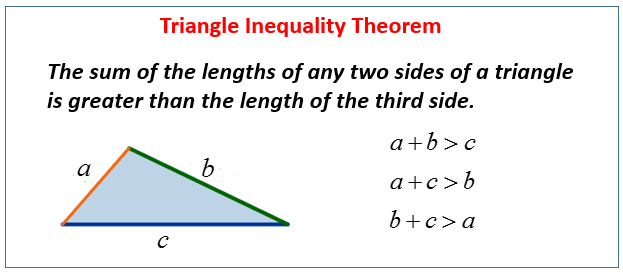
In order to simplify the problem as much as possible, we will place distinct labels on each of the three coins, such that there will be exactly \(4^3 = 64\) possible combinations of the three coins found in your pocket. This is so that when we list out the combinations of coins that can lead to strings forming triangles, we don't have to worry about double-counting any combinations as different ordering of coins form different and distinct cases. It also simplifies computation in the end as each of those 64 combinations will be equally likely to appear in your pocket. In the extension section, I will describe the second method of finding the answer without distinct labels on each of the three coins.
Since the total number of scenarios, being 64, isn't a great deal to keep track, we can apply triangle inequality and count out the number of cases that satisfy it. We can use MATLAB to help us:
function res = canBeTriangle(a, b, c)
% Given the three side lengths a, b, and c, determine whether they can
% form a closed triangle or not.
if a <= 0 || b <= 0 || c <= 0
res = false;
return;
end
% Apply triangle inequality
res = ...
a + b > c && ...
a + c > b && ...
b + c > a;
end
Then we use the "canBeTriangle" function to loop over all cases and determine which ones can form a triangle:
% Exhaustive search for number of ways to form triangles
% Riddler Express 3/5/2021
% David Ding
clear;
clc;
%% Start of script
coinSet = [1 5 10 25];
triangleWays = 0;
triangleMatrix = NaN(64, 3);
for coin1 = coinSet
for coin2 = coinSet
for coin3 = coinSet
if canBeTriangle(coin1, coin2, coin3)
triangleWays = triangleWays + 1;
triangleMatrix(triangleWays, :) = [coin1, coin2, coin3];
end
end
end
end
triangleMatrix = rmmissing(triangleMatrix);
Result:
>> triangleWays
triangleWays =
22
>> triangleMatrix
triangleMatrix =
1 1 1
1 5 5
1 10 10
1 25 25
5 1 5
5 5 1
5 5 5
5 10 10
5 25 25
10 1 10
10 5 10
10 10 1
10 10 5
10 10 10
10 25 25
25 1 25
25 5 25
25 10 25
25 25 1
25 25 5
25 25 10
25 25 25
So there are 22 ways to combine coins (with order) such that strings purchased with them can form a triangle. All combinations are listed above. Since every combination is equally likely to be found in your pocket, the probability of forming a triangle with the coins you have is simply the ratio of the number of combinations that form a triangle to the total number of possible combinations, which is \(\frac{22}{64} = \frac{11}{32}\).
So now, without exhaustively searching nor placing distinct labels on the coins, can we arrive at the answer? Well, the first step is to determine the distinct cases. That is, what is the total number of combinations of coins in your pocket, if order doesn't matter?
Here we need to do some case-by-case analysis. The mathematical interpretation of "order doesn't matter" phrase is simply the fact we are only considering which coins we have in our pocket, and how many distinct coins there are. For example, if we only choose the penny and the nickel, we would have only two cases: either we have one penny and two nickels or two pennies and one nickel.
Using this line of thinking, we break the cases down into how many distinct coins are found in each of the cases.
By inspection, there are only four cases, they are:
1 1 1 5 5 5 10 10 10 25 25 25
From our earlier analysis, there are two different combinations for every pair of coins chosen. Since we have four different coins, that leads us to \(2 \times \binom{4}{2} = 2 \times 6 = 12\) cases.
We don't have much choice here, as we simply just pick up the three coins from the set of four since we are to have three distinct coins. That gives us \(\binom{4}{3} = 4\) cases.
In total, we have \(4 + 12 + 4 = 20\) distinct cases of combinations of coins, when order doesn't matter.
Now we consider the numerator. Since the triangle inequality is made up of three inequalities that must all be satisfied, it would be easier to consider the trio of coins that do not satisfy it, since we just have to ensure one inequality is not met.
We observe that the difference between any pair from the four coins are all sufficiently large such that it would not be possible to form a triangle having three distinct coins (try it!). That means 4 out of the 20 scenarios are gone. We also observe that the cases involving only one distinct coin would always work, as an equilateral triangle would be formed. So we only need to consider the cases with two distinct coins. In this case, it is easy to see that if we have two of the smaller coin, they would never add up and exceed the larger coin (5 + 5 = 10 is close, but we need the sum to be bigger than 10). So we need for the two distinct coins case the smaller coin being unique. That leads us to \(\binom{4}{2} = 6\) cases.
In summary, the coin combinations that would form a triangle are the following two cases:
And we end up with 10 cases that form a triangle. They can be listed out as follows (again order doesn't matter):
1 1 1 5 5 5 10 10 10 25 25 25 1 5 5 1 10 10 1 25 25 5 10 10 5 25 25 10 25 25
But wait! Since now we are no longer considering individual coin combinations but rather pooling together cases where different orders are considered the same cases, each of the 20 total cases are no longer equally likely to occur, and so we cannot just write down 10/20. Instead, we need to consider the probability of each of the three scenarios occurring. Denoting \(p_k\) as the probability of having \(k\) distinct coins in your pocket, our final answer is as follows:
\begin{align} &P(\text{Three coins can buy strings that form a triangle}) & \\ &= P(\text{one distinct coin forms a triangle}) \times p_1 \\ &+ P(\text{two distinct coins form a triangle}) \times p_2 \\ &+ P(\text{three distinct coins form a triangle}) \times p_3 \\ \end{align}
The last term is going to be zero, but we can easily determine \(p_3\) and along with \(p_1\) such that \(p_2 = 1 - p_1 - p_3\). Now, \(p_1 = \frac{1}{16}\) as the probability of picking out the same coin from the second and third group, assuming each group is independent, would be \(\frac{1}{4} \times \frac{1}{4} = \frac{1}{16}\). Similarly, \(p_3 = \frac{3}{4} \times \frac{2}{4} = \frac{5}{16}\) as we only have three choices in group 2 and two choices left in the last group if we were to have 3 distinct coins. Therefore, \(p_2 = 1 - \frac{1}{16} - \frac{5}{16} = \frac{9}{16}\). Putting everything together, we have:
\begin{align} &P(\text{Three coins can buy strings that form a triangle}) & \\ &= 1 \times p_1 + \frac{1}{2} \times p_2 + 0 \times p_3 \\ &= \frac{1}{16} + \frac{9}{32} \\ &= \boxed{\frac{11}{32}} \end{align}
As expected!