



April 29, 2022
There are many fractions with a numerator of 1 whose decimal expansions don’t go on to infinitely many decimal places. For example, 1/4 is equivalent to the decimal 0.25, and 1/500 is equivalent to 0.002. However, the decimal expansion of 1/3 is 0.33333 …, a decimal that never terminates.
If you were to add up all these numbers — fractions with a numerator of 1 whose decimal expansions don’t go on forever — what would be the sum? (Note: Before you ask, let’s include the fraction 1/1 in this group.)
2.5
Explanation:
Pick a terminating decimal number, any terminating decimal number, say 0.43274369. What is its equivalent form in fractions? Well, the easiest way is to divide it by the power of 10 equal to its precision! The precision of a decimal number, as you'll see throughout this solution, is the key in finding the answer. It is simply the number of decimal places (digis after the decimal point) of a number. If it's repeating or irrational, then we would need infinite precision to represent the number. Thankfully, we are only dealing with terminating decimal places, so finite precision suffices. In the example given above, we have 8 decimal places in the number, so precision of 8 is enough and we simply represent the numer as \(43274369 / 10^8\). Très facile!
Of course, it is entirely possible that the fraction can be reduced further, but we are only interested in the value of the fraction. It is a good thing too as we would want to prevent double-counting. Therefore, Keeping everything simple, we work with fractions whose denominators that are powers of 10, reduced or not. In this case, the precision of the fraction would be loosely defined here as \(N\).
Now let's roll up our sleeves.
Let us consider the denominator of 10. This means we are looking at ALL fractions whose numerator is 1, whose decimal value has a finite precision, and whose denominator is no greater than 10. This can only be the following: 1, 1/2, 1/5, and 1/10. What do those fractions have in common? They are factors of 10. In fact, in keeping up with our simplicity setup and not reducing any fractions, we would have: 10/10, 5/10, 2/10, 1/10. Now let's increase the precision by 1 to work with denominators of 100. In addition to 100/100, 50/100, 20/100, and 10/100, which are equivalent to the fractions covered in the 10-case, we would also have 1/100, 2/100, 4/100, 5/100, and 25/100. Do you see the pattern yet?
In fact, all of the fractions whose denominator is of the form \(10^N\) for some positive integer \(N\) that can be written with terminating decimals and reduced to a fraction whose numerator is 1 MUST have the numerator as a factor of \(10^N\). The number \(10^N\) has the prime factorization of \(2^N5^N\). The sum of all factors would therefore be:
\begin{align} &\text{Sum of all factors of } 10^N \\ &=(2^0 + 2^1 + \dots + 2^N)(5^0 + 5^1 + \dots + 5^N) \\ &=\left[\frac{(2^{N+1} - 1)}{2-1}\right]\left[\frac{(5^{N+1} - 1)}{5-1}\right] \\ &=\frac{(2^{N+1} - 1)(5^{N+1} - 1)}{4} \end{align}
Where we made use of the geometric series formula above. The rationale behind the first line of equation is that when expanded, it is the sum of all possible factors of \(10^N = 2^N5^N\) whereby each term is taking some powers of 2 from 0 to N and then taking some powers of 5 from 0 to N, combining it, and get a number that is a unique factor of \(10^N\).
Therefore, for any given precision \(N\), the sum we are looking for is:
\begin{align} \frac{(2^{N+1} - 1)(5^{N+1} - 1)}{4 \times 10^N} \end{align}
However, even a terminating decimal can go up to any arbitrary precision, therefore, we must let \(N\) go to infinity here. The answer to the puzzle is simply the evaluation of the following limit:
\begin{align} \boxed{\lim_{N \to \infty} \frac{(2^{N+1} - 1)(5^{N+1} - 1)}{4 \times 10^N}} \end{align}
Let's evaluate:
\begin{align} &\lim_{N \to \infty} \frac{(2^{N+1} - 1)(5^{N+1} - 1)}{4 \times 10^N} \\ &\\ &= \lim_{N \to \infty} \frac{2^{N+1}5^{N+1} - 2^{N+1} - 5^{N+1} + 1}{4 \times 10^N} \\ &\\ &= \lim_{N \to \infty} \frac{10^{N+1} - (2^{N+1} + 5^{N+1}) + 1}{4 \times 10^N} \\ &\\ &= \frac{10^{N+1}}{4 \times 10^N} - \lim_{N \to \infty} \frac{(2^{N+1} + 5^{N+1}) - 1}{4 \times 10^N} \\ &\\ &= \frac{5}{2} - \lim_{N \to \infty} \frac{(2^{N+1} + 5^{N+1}) - 1}{4 \times 10^N} \\ \end{align}
The second term of the expression above is a limit that can be evaluated via bounding:
\begin{align} &\lim_{N \to \infty} \frac{(2^{N+1} + 5^{N+1}) - 1}{4 \times 10^N} \\ &\\ &\leq \lim_{N \to \infty} \frac{(2^{N+1} + 5^{N+1})}{10^N} \\ &\\ &\leq \lim_{N \to \infty} \frac{(5^{N+1} + 5^{N+1})}{10^N} \\ &\\ &=\lim_{N \to \infty} \frac{2 \times 5^{N+1}}{10^N} \\ &\\ &=\lim_{N \to \infty} \frac{2 \times 5 \times 5^N}{10^N} \\ &\\ &=\lim_{N \to \infty} \frac{10 \times 5^N}{10^N} \\ &\\ &=10 \times \lim_{N \to \infty} \left(\frac{1}{2}\right)^N \\ &\\ &=0 \\ \end{align}
Putting everything together:
\begin{align} &\lim_{N \to \infty} \frac{(2^{N+1} - 1)(5^{N+1} - 1)}{4 \times 10^N} \\ &\\ &= \frac{5}{2} - \lim_{N \to \infty} \frac{(2^{N+1} + 5^{N+1}) - 1}{4 \times 10^N} \\ &\\ &=\frac{5}{2} - 0\\ &\\ &=\boxed{\frac{5}{2}} = 2.5\\ \end{align}
The graph below shows how the sum converges to 2.5 as precision increases towards infinity:
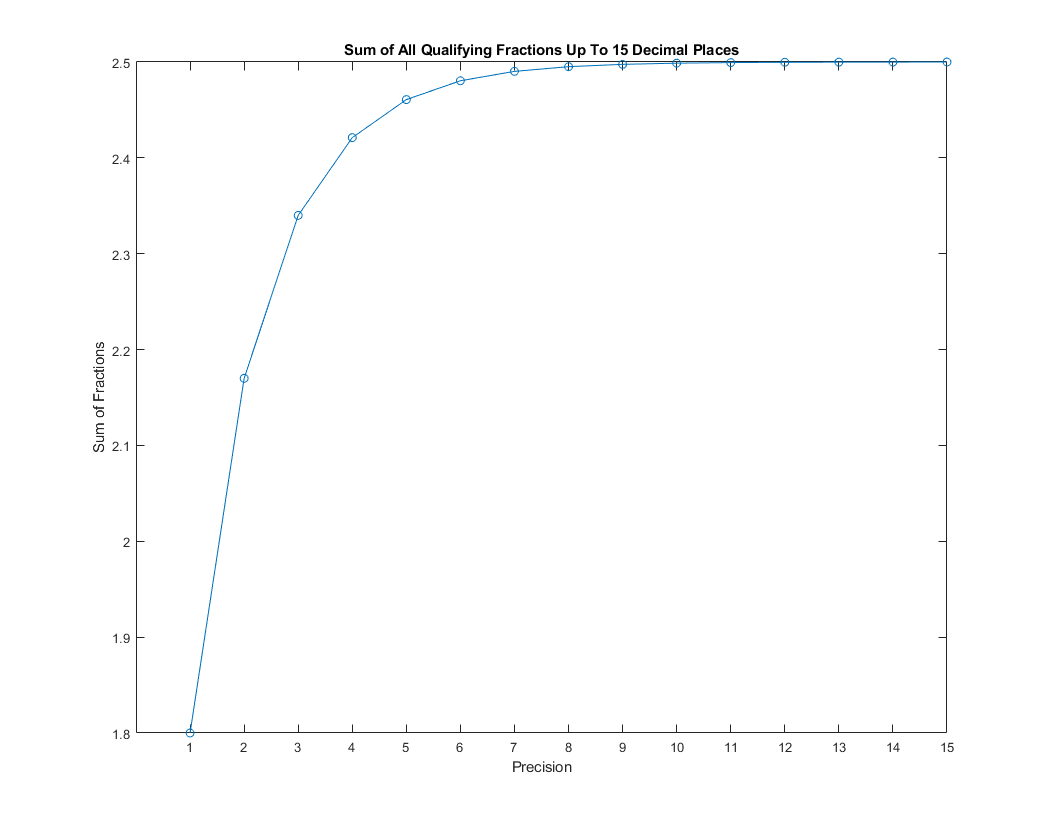
The code is written in MATLAB, and shows the build up of those fractions:
function sumOfFrac = getSum(N)
% Retrieve the sum of all terminating decimal fractions with precision
% N
sumOfFrac = 0;
for i = 0:N
for j = 0:N
denom = 2^i * 5^j;
sumOfFrac = sumOfFrac + 1/denom;
end
end
end
Of course, if 1 is excluded, then the sum still adds up to 1.5, curiously a value that is still greater than 1.