



May 17, 2021
You and your infinitely many friends are sharing a cake, and you come up with two rather bizarre ways of splitting it.
For the first method, Friend 1 takes half of the cake, Friend 2 takes a third of what remains, Friend 3 takes a quarter of what remains after Friend 2, Friend 4 takes a fifth of what remains after Friend 3, and so on. After your infinitely many friends take their respective pieces, you get whatever is left.
For the second method, your friends decide to save you a little more of the take. This time around, Friend 1 takes \(\frac{1}{2^2}\) (or one-quarter) of the cake, Friend 2 takes \(\frac{1}{3^2}\) (or one-ninth) of what remains, Friend 3 takes \(\frac{1}{4^2}\) of what remains after Friend 3, and so on. Again, after your infinitely many friends take their respective pieces, you get whatever is left.
Question 1: How much of the cake do you get using the first method?
Question 2: How much of the cake do you get using the second method?
Extra credit: Your friends are feeling rather guilty for not saving enough of the cake for you, so they try one more method. This time, they only take the fractions with even denominators from the second method. So Friend 1 takes \(\frac{1}{2^2}\) of the cake, Friend 2 takes \(\frac{1}{4^2}\) of what remains, Friend 3 takes \(\frac{1}{6^2}\) of what remains after Friend 2, and so on. After your infinitely many friends take their respective pieces, how much of the cake do you get?
Explanation:
For question 1, let's try to find a pattern by making a table:
| Friend | Cake Portion Before | Takes | Cake Portion Remaining |
|---|---|---|---|
| 1 | 1 | \(\frac{1}{2}\) | \(1 - \frac{1}{2} = \frac{1}{2}\) |
| 2 | \(\frac{1}{2}\) | \(\frac{1}{3}\) | \(\frac{1}{2} \times \left(1 - \frac{1}{3}\right) = \frac{1}{2} \times \frac{2}{3} = \frac{1}{3}\) |
| 3 | \(\frac{1}{3}\) | \(\frac{1}{4}\) | \(\frac{1}{3} \times \left(1 - \frac{1}{4}\right) = \frac{1}{3} \times \frac{3}{4} = \frac{1}{4}\) |
| 4 | \(\frac{1}{4}\) | \(\frac{1}{5}\) | \(\frac{1}{4} \times \left(1 - \frac{1}{5}\right) = \frac{1}{4} \times \frac{4}{5} = \frac{1}{5}\) |
| \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\vdots\) |
| \(n\) | \(\frac{1}{n}\) | \(\frac{1}{n+1}\) | \(\frac{1}{n} \times \left(1 - \frac{1}{n+1}\right) = \frac{1}{n} \times \frac{n}{n+1} = \frac{1}{n+1}\) |
| \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\vdots\) |
And hence, we see a pattern: when it's your Friend \(n\) who's ready to take his/her slice, what's left is \(\frac{1}{n}\) of the original cake. After your friend takes \(\frac{1}{n+1}\) of this remaining amount, \(\frac{1}{n+1}\) is the new remaining amount.
Which, of course, sucks to be you because you have infinite friends. Since \(\lim\limits_{n \to \infty} \frac{1}{n} = \boxed{0}\), you get no cake!
For question 2, let's make a similar table:
| Friend | Cake Portion Before | Takes | Cake Portion Remaining |
|---|---|---|---|
| 1 | 1 | \(\frac{1}{4}\) | \(1 - \frac{1}{4} = \frac{3}{4}\) |
| 2 | \(\frac{3}{4}\) | \(\frac{1}{9}\) | \(\frac{3}{4} \times \left(1 - \frac{1}{9}\right) = \frac{3}{4} \times \frac{8}{9} = \frac{2}{3}\) |
| 3 | \(\frac{2}{3}\) | \(\frac{1}{16}\) | \(\frac{2}{3} \times \left(1 - \frac{1}{16}\right) = \frac{2}{3} \times \frac{15}{16} = \frac{5}{8}\) |
| 4 | \(\frac{5}{8}\) | \(\frac{1}{25}\) | \(\frac{5}{8} \times \left(1 - \frac{1}{25}\right) = \frac{5}{8} \times \frac{24}{25} = \frac{3}{5}\) |
| \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\vdots\) |
Here there doesn't seem to be much of a pattern going on, so we directly write out the expression of the amount of cake remaining after \(n\) friends have taken the cake, as below:
\begin{align} &\text{Cake Remaining After n Friends}\\ &= \left(1 - \frac{1}{2^2}\right) \times \left(1 - \frac{1}{3^2}\right) \times \left(1 - \frac{1}{4^2}\right) \times \dots \times \left(1 - \frac{1}{(n+1)^2}\right) \\ &= \left(\frac{2^2 - 1}{2^2}\right) \times \left(\frac{3^2 - 1}{3^2}\right) \times \left(\frac{4^2 - 1}{4^2}\right) \times \dots \times \left(\frac{(n+1)^2 - 1}{(n+1)^2}\right) \\ &= \left(\frac{1 \times 3}{2^2}\right) \times \left(\frac{2 \times 4}{3^2}\right) \times \left(\frac{3 \times 5}{4^2}\right) \times \dots \times \left(\frac{(n \times (n+2)}{(n+1)^2}\right) \\ \end{align}
Do you see a pattern? Yes, except for the last multiplicant in \(n\), all other multiplicants will have their denominators completely canceled out--once by the neightbor before it and once after. For example, in \(\left(\frac{3^2 - 1}{3^2}\right)\), the \(3^2\) at the bottom has, unsuprisingly, two factors of 3. One of the "3" can be canceled out by the corresponding numerator in \(\left(\frac{1 \times 3}{2^2}\right)\) and the other by that in \(\left(\frac{3 \times 5}{4^2}\right)\). Only surviving terms will be one of the factors in \(2^2\) in the first term (since there's no multiplicants before that to cancel things out), and one of the factors in \((n+1)^2\) because no multiplicants come after that. However, we let \(n \to \infty\), and so the cake portion remaining for you will be \(\boxed{\frac{1}{2}}\).
For extra credit, we will get straight to the chase similar to that for question 2, and write out the expression for the cake remaining after \(n\) friends have taken it.
\begin{align} &\text{Cake Remaining After n Friends}\\ &= \left(1 - \frac{1}{2^2}\right) \times \left(1 - \frac{1}{4^2}\right) \times \left(1 - \frac{1}{6^2}\right) \times \dots \times \left(1 - \frac{1}{(2n)^2}\right) \\ &= \left(\frac{2^2 - 1}{2^2}\right) \times \left(\frac{4^2 - 1}{4^2}\right) \times \left(\frac{6^2 - 1}{6^2}\right) \times \dots \times \left(\frac{(2n)^2 - 1}{(2n)^2}\right) \\ &= \left(\frac{1 \times 3}{2^2}\right) \times \left(\frac{3 \times 5}{4^2}\right) \times \left(\frac{5 \times 7}{6^2}\right) \times \dots \times \left(\frac{(2n-1) \times (2n+1)}{(2n)^2}\right) \\ \end{align}
Here we don't have numbers cancelling each other out nicely, so we let \(n \to \infty\) and see if we can scope out a pattern.
\begin{align} &\text{Cake Remaining After Infinite Friends}\\ &= \left(\frac{1 \times 3}{2^2}\right) \times \left(\frac{3 \times 5}{4^2}\right) \times \left(\frac{5 \times 7}{6^2}\right) \times \dots \\ &= \left(\frac{1^2 \times 3^2 \times 5^2 \times 7^2 \times 9^2 \times \dots}{2^2 \times 4^2 \times 6^2 \times 8^2 \times 10^2 \times \dots}\right) \\ \end{align}
Oh ho ho! What do we have here? Talk about battle of sexes. Here we have a feud between the sum of odd squares and even squares. Thankfully, we have the Wallis Product.
\begin{align} &\text{Cake Remaining After Infinite Friends}\\ &= \left(\frac{1 \times 3}{2^2}\right) \times \left(\frac{3 \times 5}{4^2}\right) \times \left(\frac{5 \times 7}{6^2}\right) \times \dots \\ &= \left(\frac{1^2 \times 3^2 \times 5^2 \times 7^2 \times 9^2 \times \dots}{2^2 \times 4^2 \times 6^2 \times 8^2 \times 10^2 \times \dots}\right) \\ &= \frac{1}{\text{Wallis Product}} \\ &= \boxed{\frac{2}{\pi}} \\ &\approx 0.637 \end{align}
Suspending the belief of someone having infinite friends (he/she must be really popular!), let's try to solve each question by putting words into numbers. For Question 1, your friends really like cake and so they take portions without reserve, leaving you with imaginably a very small portion. Just how small depends on how much your friends plan on taking. Let's start with Friend 1. Right off the bat he/she takes half of the cake! However, Friend 2 takes considerably less as he/she only takes \(\frac{1}{2} \times \frac{1}{3} = \frac{1}{6}\) and NOT just \(\frac{1}{3}\) (otherwise going down this path one cake would not be enough thanks to the divergence of harmonic series). Continuing this trend, your Friend #3 takes a measly \(\frac{1}{6} \times \frac{1}{4} = \frac{1}{24}\) of the whole cake, and Friend 5 takes just \(\frac{1}{120}\) of the entire cake! Just five friends in and it's looking like your many friends who are still waiting in queue will be taking portions of this delicious cake at atomic levels, even if the cake were the size of the entire planet Earth. If you still want decent portions of this treat, things are certaining turning promising. But--you do have an infinite number of friends, so maybe not?
The total portions of the cake your entire infinite list of friends will be taking can be express as below:
\begin{align} \text{Your friends' portions} &= \frac{1}{2} + \frac{1}{2} \times \frac{1}{3} + \frac{1}{2} \times \frac{1}{3} \times \frac{1}{4} + \dots \\ &= \frac{1}{2} + \frac{1}{2 \times 3} + \frac{1}{2 \times 3 \times 4} + \dots \\ &= \frac{1}{2!} + \frac{1}{3!} + \frac{1}{4!} + \dots \\ &= \sum_{k = 2}^\infty \frac{1}{k!} \end{align}
A simple comparison test with the following geometric series:
\begin{equation} \sum_{k = 1}^\infty \frac{1}{2^k} = 1 \end{equation}
will reveal that your entire friends' portions taken will be finite, first of all, and will also be less than 1, meaing, in the end (if there is an end to all the cake-taking), you will have some left for your own enjoyment. Now let's evaluate exactly how much your friend will be taking.
Recall from one of my earlier blogs on power series, the Taylor Series expansion of \(f(x) = e^x\) about \(x = 0\) is given below:
\begin{equation} e^x = \sum_{n=0}^\infty \frac{x^n}{n!} = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \dots \end{equation} In particular, for \(x=1\), we have: \begin{equation} e = 2 + \frac{1}{2!} + \frac{1}{3!} + \frac{1}{4!} + \dots \approx 2.7183 \end{equation}
Hence, your friends are taking in total \((e - 2) \approx 0.7183\) of the entire cake, or just under 72%.
Which means, you will be getting \(1 - (e - 2) = \boxed{3 - e} \approx 0.2817\) of the entire cake, or just above 28%. Interestingly, since \(3 - e > \frac{1}{6} \approx 0.167\), you will actually be getting the second largest portion of the cake, after Friend #1! Frankly, I can't see why you are even complaining!
Similarly, for Question 2 and Extra Credit, we write out the corresponding infinite series expression based on the puzzle description, and try to evaluate the series. Certainly, by comparison tests, those series will converge. Unfortunately, unlike question 1, those expressions do not have analytic answers, so Wolfram Alpha to the rescue again.
For Question 2:
\begin{align} \text{Your friends' portions} &= \frac{1}{2} + \frac{1}{2^2} \times \frac{1}{3^3} + \frac{1}{2^2} \times \frac{1}{3^2} \times \frac{1}{4^2} + \dots \\ &= \frac{1}{2^2} + \frac{1}{2^2 \times 3^2} + \frac{1}{2^2 \times 3^2 \times 4^2} + \dots \\ &= \frac{1}{2!^2} + \frac{1}{3!^2} + \frac{1}{4!^2} + \dots \\ &= \sum_{k = 2}^\infty \frac{1}{(k!)^2} \\ &\approx 0.280 \end{align}
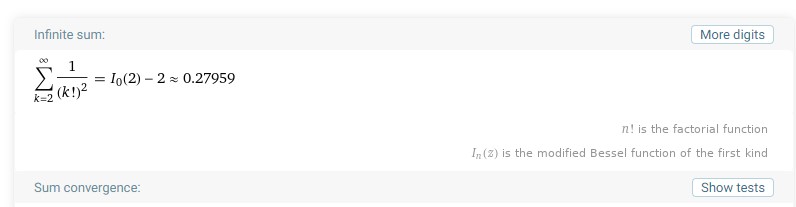
And so you will be snatching a whopping 72% of the entire cake if your friends decided to be "generous".
For Extra Credit
\begin{align} \text{Your friends' portions} &= \frac{1}{2} + \frac{1}{2^2} \times \frac{1}{4^3} + \frac{1}{2^2} \times \frac{1}{4^2} \times \frac{1}{6^2} + \dots \\ &= \frac{1}{2^2} + \frac{1}{2^2 \times 4^2} + \frac{1}{2^2 \times 4^2 \times 6^2} + \dots \\ &= \sum_{k = 1}^\infty \frac{1}{((2k)!)^2} \\ &\approx 0.252 \end{align}
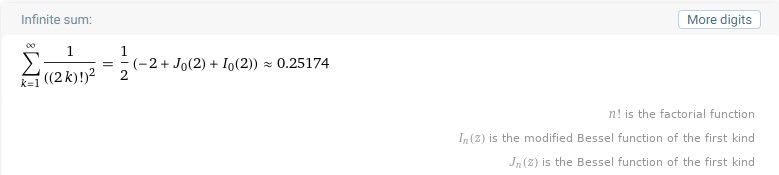
And so you will be snatching a whole 75% of the entire cake if your friends decided to be even more magnanimous.