



August 13, 2021
From Brad Fortner comes a puzzle for the cleverest among us:
You are very clever when it comes to solving Riddler Express puzzles. You are so clever, in fact, that you are in the top 10 percent of solvers in Riddler Nation (which, as you know, has a very large population). You don’t know where in the top 10 percent you are — in fact, you realize that you are equally likely to be anywhere in the topmost decile. Also, no two people in Riddler Nation are equally clever.
One Friday morning, you walk into a room with nine members randomly selected from Riddler Nation. What is the probability that you are the cleverest solver in the room?
Probability: \(\frac{6513215599}{10000000000} \approx 65.13\%\).
Explanation:
One way to start digging towards the answer is to play a little thought experiment. Suppose the nine other people in the room are also in the top 10 percentile, then what is the probability that you are the cleverest? Since you don't know your standing in the top 10 percent, the answer would be 1/10. Pretty straightforward right? Continuing this line of thought, if you know that you are among one of \(1 \leq n \leq 10\) people in the room that is in the top 10 percent of the cleverest Riddler solvers, the probability that you are the cleverest would be 1/n.
The remaining task would then be to figure out the probability of the number of others in the room who are also in the top 10 percent. This can be modeled using binomial distribution. Assuming each person's standing is indepenent of the others, and each person (besides you) has a uniform distribution of percentiles that his/her cleverness determines. Let \(X\) be the random variable representing the number of other people in the room who are in the top 10 percent. \(X\) would be binomially distributed with parameters \(N = 9\) and \(p = \frac{1}{10}\).
Putting everything together, we have:
\begin{align} &P(\text{You are the cleverest})\\ &= \sum_{k = 0}^9 \frac{1}{k+1} P(X=k) \\ &= \left.\sum_{k = 0}^9 \frac{\binom{N}{k} p^k (1-p)^{N-k}}{k+1}\right|_{N = 9,\quad p = \frac{1}{10}} \\ &= \sum_{k = 0}^9 \frac{\binom{9}{k} \left(\frac{1}{10}\right)^k \left(\frac{9}{10}\right)^{9-k}}{k+1} \end{align}
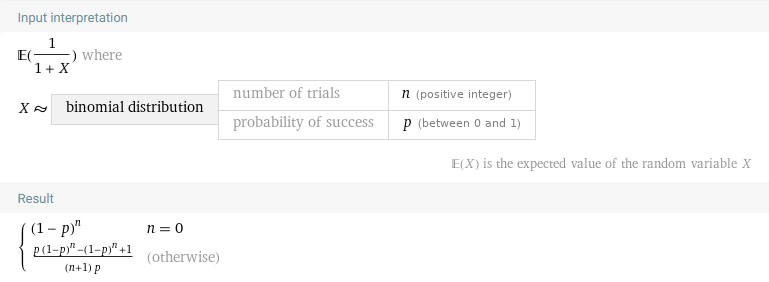
We can either evaluate the above expression directly, or realize that the expression is just \(\mathbb{E}\left[\frac{1}{X+1}\right]\). Using the second method and Wolfram alpha, we get:
\begin{align} &P(\text{You are the cleverest})\\ &= \mathbb{E}\left[\frac{1}{X+1}\right] \\ &= \left.\frac{p(1-p)^N - (1-p)^N + 1}{(N + 1)p}\right|_{N = 9,\quad p = \frac{1}{10}} \\ &= \frac{\left(\frac{1}{10}\right)\left(\frac{9}{10}\right)^9 - \left(\frac{9}{10}\right)^9 + 1}{\frac{10}{10}} \\ &= \boxed{1 - \left(\frac{9}{10}\right)^{10}} \\ &= \boxed{\frac{6513215599}{10000000000}} \\ &\approx 65.13\% \end{align}
The answer is NOT close to 100%, as one might intuitively think. This is because as sample population increases, the variability in data, in this case the rankings of the Riddler solvers, also expands. Since as long as one Riddler is also among the top 10 percent for you to have at most 50% chance of being the cleverest in the room, and we have nine guests to compete with you, you are lucky to even have a greater than 50% chance of being the cleverest!