



August 21, 2021
Help, there’s a cricket on my floor! I want to trap it with a cup so that I can safely move it outside. But every time I get close, it hops exactly 1 foot in a random direction.
I take note of its starting position and come closer. Boom — it hops in a random direction. I get close again. Boom — it takes another hop in a random direction, independent of the direction of the first hop.
What is the most probable distance between the cricket’s current position after two random jumps and its starting position? (Note: This puzzle is not asking for the expected distance, but rather the most probable distance. In other words, if you consider the probability distribution over all possible distances, where is the peak of this distribution?)
Most probable value: 2 feet.
Explanation:
We can model this problem by treating the position of the cricket's jump as a random length-1 complex number. That is, the final jump can be represented by the number \(e^{i\theta}\), where \(\theta\) is a uniformly distributed real number between 0 and \(2\pi\) representing the angle of the complex number. The complex number will be on the unit circle, but its position on the circle will depend on the value of \(\theta\), its argument.
The second jump is once again a random \(e^{i\theta}\) where \(\theta \sim U (0, 2\pi)\). The final position of the cricket will simply be represented by the sum of those two complex numbers, where the distance would be the magnitude of the sum.
Letting the first angle be \(\theta_1\), and the second angle be \(\theta_2\), both independently and identically distributed (i.i.d) as \(\sim U (0, 2\pi)\), the final jump's position is represented by the complex number \(e^{i\theta_1} + e^{i\theta_2}\).
Thanks to Euler's formula, we can convert each of the terms in the sum into its rectangular form and extract the expression for distance:
\begin{align} &\text{Final distance of the cricket's jump}\\ &= | e^{i\theta_1} + e^{i\theta_2} |\\ &= | \cos{\theta_1} + i\sin{\theta_1} + \cos{\theta_2} + i\sin{\theta_2} |\\ &= \sqrt{(\cos{\theta_1} + \cos{\theta_2})^2 + (\sin{\theta_1} + \sin{\theta_2})^2} \\ &= \sqrt{\cos^2{\theta_1} + \cos^2{\theta_2} + \sin^2{\theta_1} + \sin^2{\theta_2} + 2\cos{\theta_1}\cos{\theta_2} + 2\sin{\theta_1}\sin{\theta_2}} \\ &= \sqrt{1 + 1 + 2(\cos{\theta_1}\cos{\theta_2} + \sin{\theta_1}\sin{\theta_2})} \\ &= \sqrt{2(1 + \cos{\theta_1}\cos{\theta_2} + \sin{\theta_1}\sin{\theta_2})} \\ &= \sqrt{2(1 + \cos{(\theta_1 - \theta_2)})} \\ \end{align} Leveraging some useful trig identities.
Before proceeding, let's do some sanity checks on the above expression for the final distance. We know that the range of \(\cos\) is between -1 and 1, and so the above expression ranges between 0 and 2. The final distance of the cricket is minimized to 0, if the two angles are \(\pi\) apart. This makes sense as it represents the cricket essentially performing a u-turn. The distance is maximized, however, when the difference between the two angles is 0, which represents the cricket doing two hops in the same direction. Since no component is wasted, the distance is maximized. We cross-reference the values of \(\cos\) and find out that \(\cos{0} = 1\) and \(\cos{\pi} = -1\), which makes the distance expression 2 and 0, respectively. Everything checks out so far.
Now, We know how the \(\theta\)s are distributed. However, obtaining the probability density function (pdf) of the distance expression would require some pretty complicated transformations using calculus. However, taking a closer look at the puzzle and we realize that we just need to find the most probable value. Since the expression is completely determined by \((\theta_1 - \theta_2)\), we can simply look at the most probable value of that random variable, and plug in the value to obtain our answer.
Whenever we have two random variables, assuming they are independent, the pdf of their linear combinations is simply the convolution of the individual pdfs. Even simpler here is that the pdfs of those \(\theta\)s are just rectangles, since they are uniformly distributed. The convolution of two rectangles is a triangle, and so we have a hope of finding the distinct global maximum of the resulting pdf, thereby obtaining us the answer.
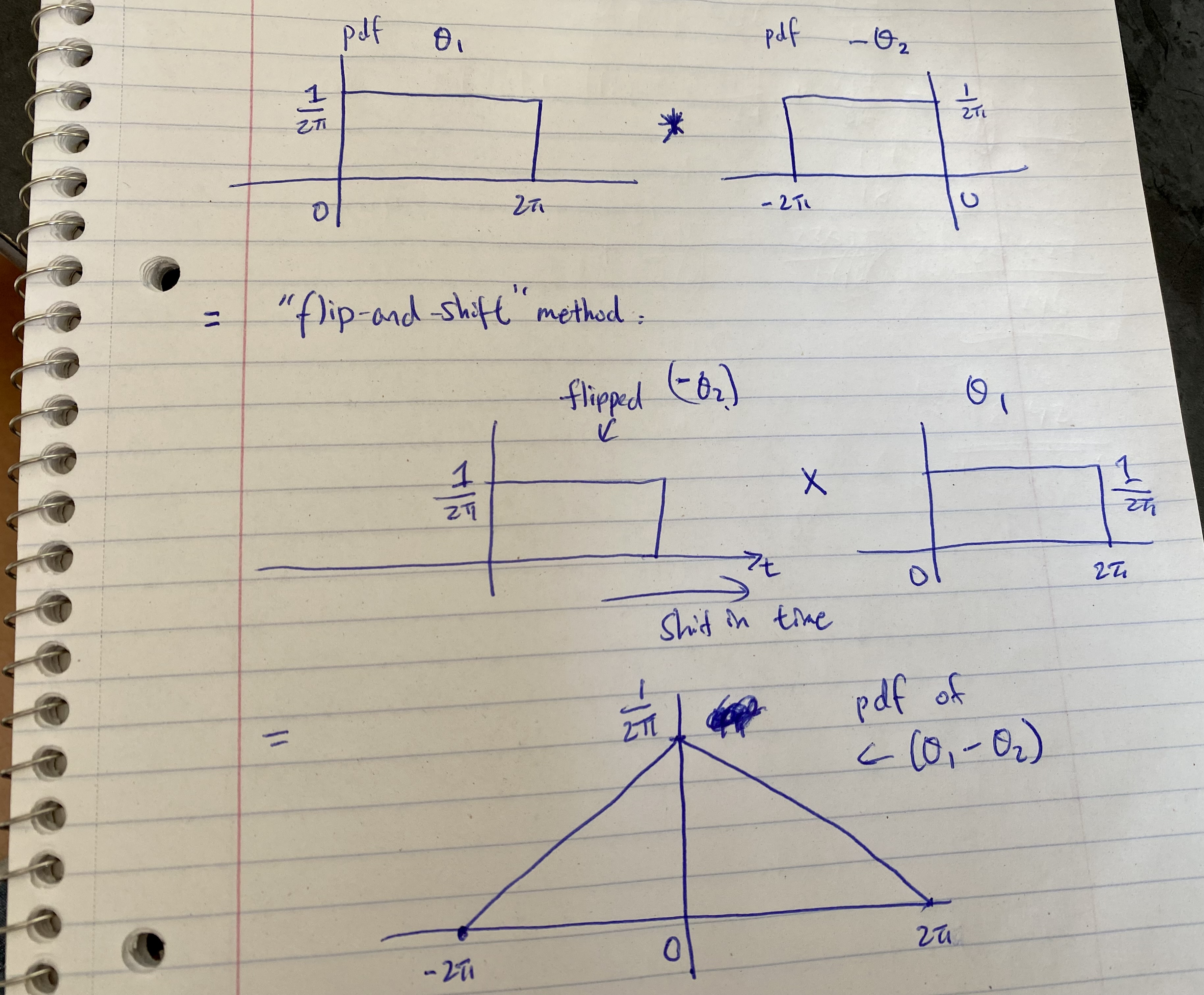
(As someone with background in Signal Processing, convolution is almost second nature...hopefully this is not too confusing!)
Moving on, looking at the pdf of \((\theta_1 - \theta_2)\), it is clear that the most probable value is when \((\theta_1 - \theta_2) = 0\). We substitute this value in our earlier expression for distance and obtain the most probable distance:
\begin{align} &\text{Most probable distance}\\ &= \sqrt{2(1 + \cos{(\theta_1 - \theta_2)})} |_{(\theta_1 - \theta_2)=0} \\ &= \sqrt{2(1 + \cos{0})} \\ &= \sqrt{2(1 + 1)} \\ &= \sqrt{4} \\ &= \boxed{2} \end{align}
A quick simulation reveals the actual pdf of the distance expression, along with the fact that the mode of the distribution is indeed 2:
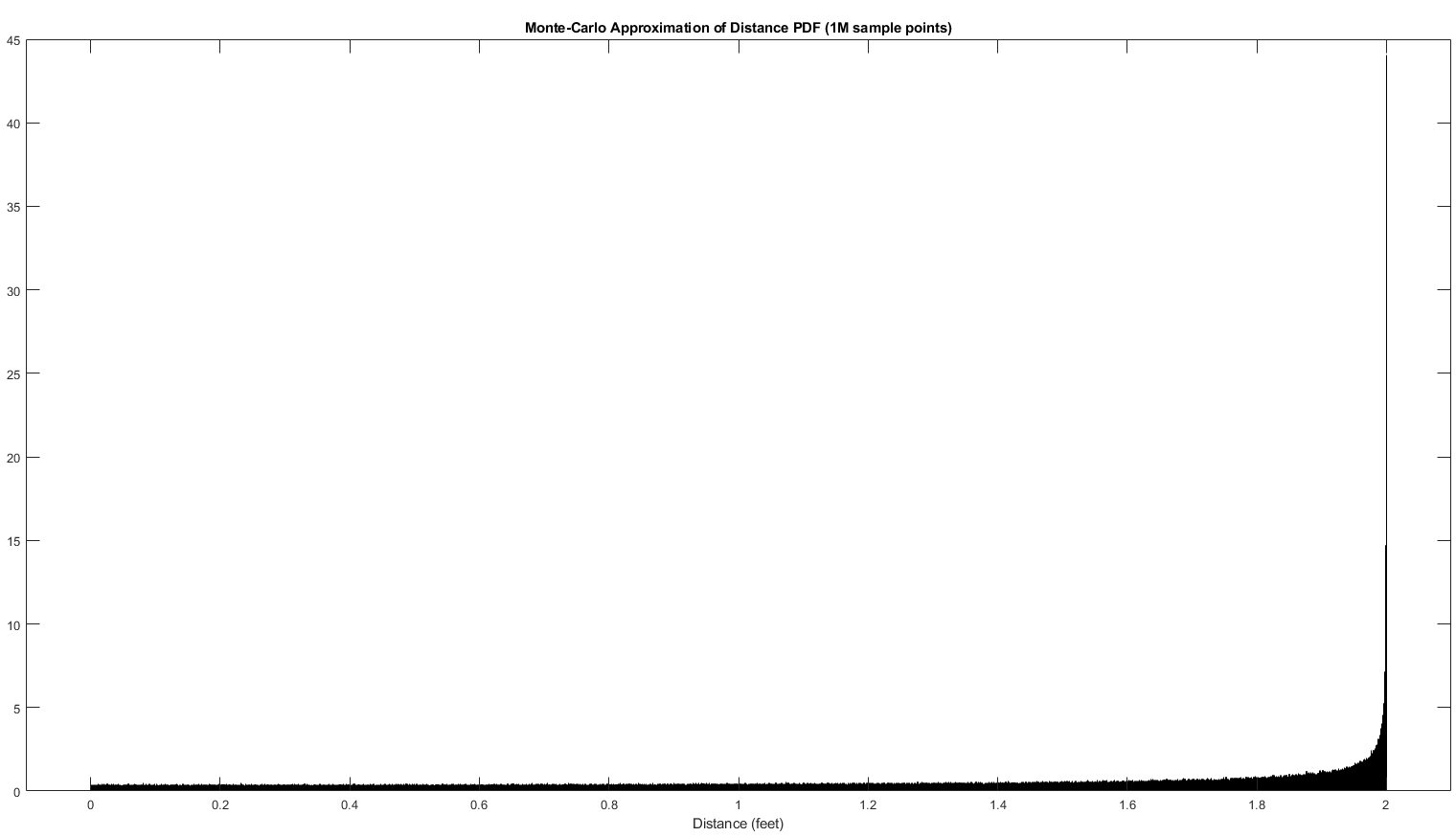
Technically speaking, since the distribution of the distance here is continuous, any *one* value has a 0 probability of being realized. Therefore for this puzzle, by most probable, we are simply looking at the peak of the pdf of the distribution, defining its "mode". One way to interpret this data is that the cricket will more likely to advance from its starting location than to backtrack.