



September 17, 2021
I recently came across a rather peculiar recipe for something called Babylonian radish pie. Intrigued, I began to follow the directions, which said I could start with any number of cups of flour.
Any number? I mean, I had to start with some flour, so zero cups wasn’t an option. But according to the recipe, any positive value was fair game. Next, I needed a second amount of flour that was 3 divided by my original number. For example, if I had started with two cups of flour, then the recipe told me I now needed 3 divided by 2, or 1.5, cups at this point.
I was then instructed to combine these amounts of flour and discard half. Apparently, this was my new starting amount of flour. I was to repeat the process, combining this amount with 3 divided by it and then discarding half.
The recipe told me to keep doing this, over and over. Eventually, I’d have the proper number of cups of flour for my radish pie.
How many cups of flour does the recipe ultimately call for?
Convergence value: \(\sqrt{3} \approx 1.732\) cups.
Explanation:
There are three ways to solve the problem: algebraic, emprical, and intuitive. The first two methods will shed light on the answer while the last one will shed light on the pattern and the general answer for more arbitrary baking instructions. Let's look at each one of them!
Let \(F_n\) denote the cups of flour at step \(n\). That is, \(F_0 = n\) as the starting value while \(F_n = \frac{F_{n-1} + 3/F_{n-1}}{2}\) as instructed for \(n > 0\). Now, assuming the sequence \(\{F_0, F_1, F_2, \dots F_n, \dots \}\) converges, then at some large value of \(n\), we should essentially get \(F_n = F_{n+1}\). That is, doing this mysterious mixing of flours won't yield a new value for the cups of flours now obtained. Let's denote that limiting value to be \(F\). Then, writing out the equation we essentially have:
\begin{align} F &= \frac{F + 3/F}{2} \\ 2F &= F + \frac{3}{F} \\ 2F &= \frac{F^2 + 3}{F} \\ 2F^2 &= F^2 + 3 \\ F^2 &= 3 \\ F &= \boxed{\sqrt{3}} \approx 1.73 \end{align}
As we ignore the negative solution.
So it appears that in the end this Babylonian radish pie requires \(\sqrt{3}\) cups of flour. Let's check for different starting cups of flour and see if they all converge to this value. It turns out the convergence is pretty fast and steadfast:
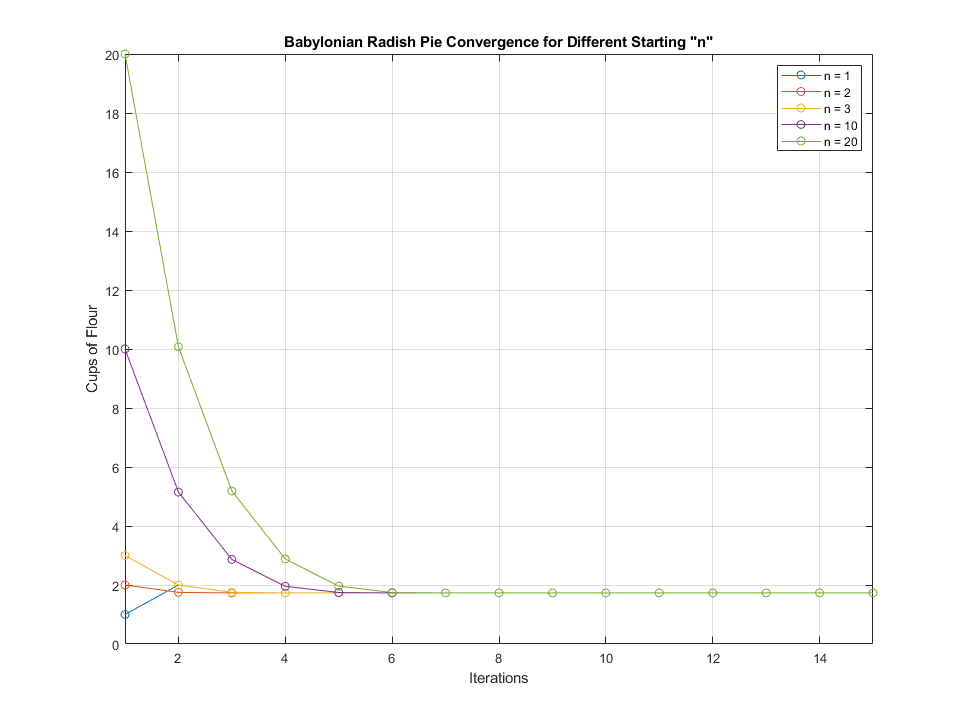
Keep in mind, \(\sqrt{3} \approx 1.73\). This value is essentially reached for our sample cases after only six rounds of mixing.
After doing the math and double-checking with simulations, the question becomes "Why?". Why does this mysterious recipe eventually calls for \(\sqrt{3}\) cups of flour? Let us recap the instructions first:
Going from one step to the other, there are three substeps: 1) Noting the previous cup amount. 2) Introducing the new amount as 3 divided by the previous amount. 3) Taking the average of the two amounts as the new amount for the next step.
Now let's think about the old amount and call it \(F_1\). If \(F_1 < \sqrt{3}\), then \(3/F_1 > \sqrt{3}\). Then, \(F_2 = \text{Average of } F_1 \text{ and } 3/F_1\) will bring both values closer to \(\sqrt{3}\) since each value are on either side of the converging value. This is also true if \(F_1 > \sqrt{3}\), as then \(3/F_1 < \sqrt{3}\). Only when \(F_1 = \sqrt{3}\) does \(3/F_1 = \sqrt{3}\) also, at which point \(F_2\) is simply \(\sqrt{3}\) as well. This flour-mixing instruction is actually a multiple-step averaging process with the targeted average value eventually being \(\sqrt{3}\).
With this knowledge, we can generalize the flour-mixing instruction. Suppose our new Babylonian radish pie calls for any positive starting amount, and we then add \(T\) divided by that amount to it and discarding half. Then, the balancing value becomes \(\sqrt{T}\) for the exact reason as when \(T = 3\) for the original puzzle, and for the general case we will eventually require \(\sqrt{T}\) cups of flour.
Happy Baking!