



September 24, 2021
While watching batter spread out on my waffle iron, and thinking back to a recent conversation I had with Friend-of-The-Riddler™ Benjamin Dickman, I noticed the following sequence of numbers:
1, 4, 4, 0, 4, 8, 0, 0, 4, 4, 8, …
I was then instructed to combine these amounts of flour and discard half. Apparently, this was my new starting amount of flour. I was to repeat the process, combining this amount with 3 divided by it and then discarding half.
Before you ask — yes, you can find this sequence on the On-Line Encyclopedia of Integer Sequences. However, for the full Riddler experience, I urge you to not look it up. See if you can find the next few terms in the sequence, as well as the pattern.
Now, for the actual riddle: Once you’ve determined the pattern, can you figure out the average value of the entire sequence?
Average value: \(\pi\)
Explanation:
The batter spreading out from the waffle iron gave away the punchline: the pattern on the iron can represent "integer" points on a Cartesian plane, while the batter, assuming poured uniformly, will spread out in a circular pattern. Upon seeing this, Zach thought of the sequence given in the puzzle. Then, it must be the number of those lattice points hit by the expanding batter, as the batter grows its radius!
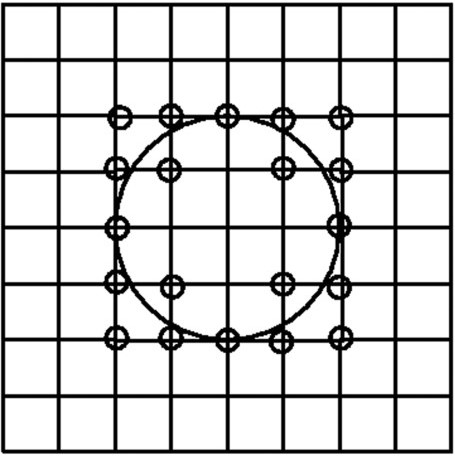
Specifically, this sequence, starting with \(n = 0\), is the number of lattice points that fall on the circle with radius of \(\sqrt{n}\). A lattice point is a point in the Cartesian plane whose coordinates are integers. In other words, it is the number of integer solutions \((x, y)\) that satisfy the equation \(x^2 + y^2 = n\) with \((x, y)\) being an ordered pair. For example, for \(n = 0\), we essentially have one point \((0, 0)\) being on this circle of radius 0 at the origin. When \(n = 1\), we have four points: \((0, 1), (0, -1), (1, 0), (-1, 0)\). Denoting the sequence as \(a_n\), we therefore get \(a_0 = 0\) and \(a_1 = 4\). Similarly, for \(n = 2\), we have the points \((\pm1, \pm1)\) yielding four lattice points as well.
Now the question comes, what is the "average" of \(a_n\)?
Before diving into the problem, we need to make sense of what "average" of a sequence means. It is actually defined as a limit:
\begin{align} &\text{Average of } a_n\\ &= \lim_{n \to \infty} \frac{1}{n}\sum_{k = 0}^n a_n \end{align}
In other words, as we add up more and more values of our sequence and divide by the number of sequence terms we've added, does that value converge to some magical number?
For an n by n grid, how many lattice points are either on or in the grid?

If we have a 1 by 1 grid, the four vertices of the square are the lattice points, and so we have 4 in total. If we have a 2 by 2 grid, as the figure above shows, then we have 9 lattice points in total. In short, if we have an n by n grid, it seems that we have \((n+1)^2\) lattice points in total. We can in fact prove this in many ways, and here I will show via induction.
We've already shown the base case of 1 by 1 grid. Now assume for an n by n grid there are \((n+1)^2\) lattice points in total, then for an (n+1) by (n+1) grid, we add an extra row of grids at the bottom of the n by n grid, an extra column to the right, and an extra grid at the bottom right. If you are willing to visualize with me, that's an extra row of (n+1) lattice points at the bottom, an extra column of (n+1) lattice points to the right, and an extra lattice point at the bottom right. Using our hypothesis of \((n+1)^2\) lattice points for the n by n grid, for the (n+1) by (n+1) grid we have a total of \((n+1)^2 + 2(n+1) + 1\) = \((n+2)^2\) lattice points. Hence by mathematical induction our hypothesis is proven.
For a grid of \(n\) by \(n\) where \(n\) is an integer, there are \((n+1)^2\) lattice points either on or inside the grid.
Now we have assembled all the ingredients to solve the average question. Denote a new sequence \(s_n = \sum_{k = 0}^n a_n\). Geometrically, \(s_n\) represents the total number of lattice points either on or inside the circle with the equation \(x^2 + y^2 = n\). Now let us consider a \((2\sqrt{n})\) by \((2\sqrt{n})\) square centered at the origin just encompassing the circle \(x^2 + y^2 = n\), as seen below:
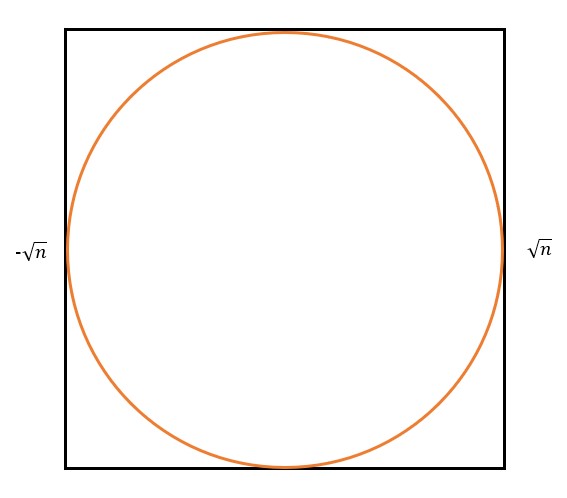
The area of the square is obviously \((2\sqrt{n})^2 = 4n\), and the area of the circle, with the radius being \(\sqrt{n}\), is obviously \(\pi (\sqrt{n})^2 = \pi n\). Therefore, the ratio of the area of the circle to that of the square just enclosing it is \(\pi : 4\). Going the distance, if \(n\) is inconceivably large, having a gigantic \(G\) number of lattice points either on or inside of it, then we can say with confidence that there are \(\frac{\pi}{4} G\) lattice points on or inside the circle. Proportions everybody!
We are now getting closer. How many lattice points are there roughly on or inside the square with side length of \((2\sqrt{n})\)? From our results earlier, that would be \((2\sqrt{n} + 1)^2\). How many would be on or inside the circle? Roughly \(\frac{\pi}{4}\) of that. We get:
\begin{align} &\text{Average of } a_n\\ &= \lim_{n \to \infty} \frac{1}{n}\sum_{k = 0}^n a_n \\ &= \lim_{n \to \infty} \frac{1}{n} s_n \\ &= \lim_{n \to \infty} \frac{1}{n} \left(\frac{\pi}{4} \left(2\sqrt{n} + 1\right)^2 \right) \\ &= \lim_{n \to \infty} \frac{1}{n} \left(\frac{\pi}{4} \left(4n + 4\sqrt{n} + 1\right) \right) \\ &= \lim_{n \to \infty} \frac{1}{n} (\pi n + O(\sqrt{n})) \\ &= \lim_{n \to \infty} \pi + \frac{O(\sqrt{n})}{n} \\ &= \pi + \lim_{n \to \infty} \frac{O(\sqrt{n})}{n} \\ &= \pi + 0 \\ &= \boxed{\pi} \\ \end{align}
Where "\(O(\sqrt{n})\)" denotes a term that grows on the order of \(\sqrt{n}\). We don't care about the exact expression, as when we evaluate \(\lim_{n \to \infty} \frac{O(\sqrt{n})}{n}\), we note that something growing on the order of square root is slower than on the order of itself (linear growth). This means as \(n \to \infty\), the value of \(n\) will be inconceivably larger than \(\sqrt{n}\), making that fraction essentially going to 0.
So it turns out that, fittingly, the average of our circular sequence is \(\pi\). Math is beautiful, isn't it?