



October 8, 2021
From Quoc Tran comes a riddle that takes us back … to the future!
Channeling your inner Marty McFly, you travel one week back in time in an attempt to win the lottery. It’s worth $10 million, and each ticket costs a dollar. Note that if you win, your ticket purchase is not refunded. All of this sounds pretty great.
The problem is, you’re not alone. There are 10 other time travelers who also know the winning numbers. You know for a fact that each of them will buy exactly one lottery ticket. Now, according to the lottery’s rules, the prize is evenly split among all the winning tickets (i.e., not evenly among winning people). How many tickets should you buy to maximize your profits?
You should by 9990 tickets to win $9,980,010, or 99.8% of the entire jackpot share.
Explanation:
Let's first solve a few simple cases to get a feel of the problem. Suppose you, like your time-travelling companions, only purchase 1 ticket. How much is your winning? The answer is simply \((10M/11) - 1\) which is practically \(10M/11\), or about $909,000.
However, you are not a millionaire yet, and winning just under 10% after going through all that trouble building a time machine and other meticulous and tedious planning seems to be quite underwhelming. Seeing the cost of a lottery ticket is only $1, you decide to shell out an extra buck and purchase 2 tickets. All of a sudden, you are winning \((10M \times 2/12) - 2\) or about $1,667,000.
All of a sudden for an extra buck you seem to have significantly increased your winnings. Pity those time-travellers who can only afford 1 ticket! Excited about your discovery, you decide to go for three tickets. Nay, four tickets. Scratch that, five, six, ...
After all, each ticket only costs a dollar, and each extra ticket seems to drastically increase the share of the jackpot that you are earning. However, as you purchase more and more of them, you realize the cost of purchasing those tickets DO make a dent towards your winnings as you do not receive the purchase cost back into your wallet. So if you buy, say 1 million tickets, that's a cool mil off your bank account!
Therefore, the takeaway for your time-travelling heist is that there is a tradeoff: if you purchase too few tickets, you do not get the maximum amount of the jackpot share. However, if you purchase too many tickets, the cost of the tickets will start to eat away at your earnings. There is a magical number of tickets that will maximize your winnings.
We start by expressing your lottery earnings model as a function of \(x\), denoting the number of tickets you purchase. By the rules, we have:
\begin{align} f(x) &= 10^7 \left(\frac{x}{10+x}\right) - x \\ \end{align}
Plotting the function for \(x\) between 1,000 and 100,000 clearly yields the tradeoff with a clear maximal point around \(x = 10000\):
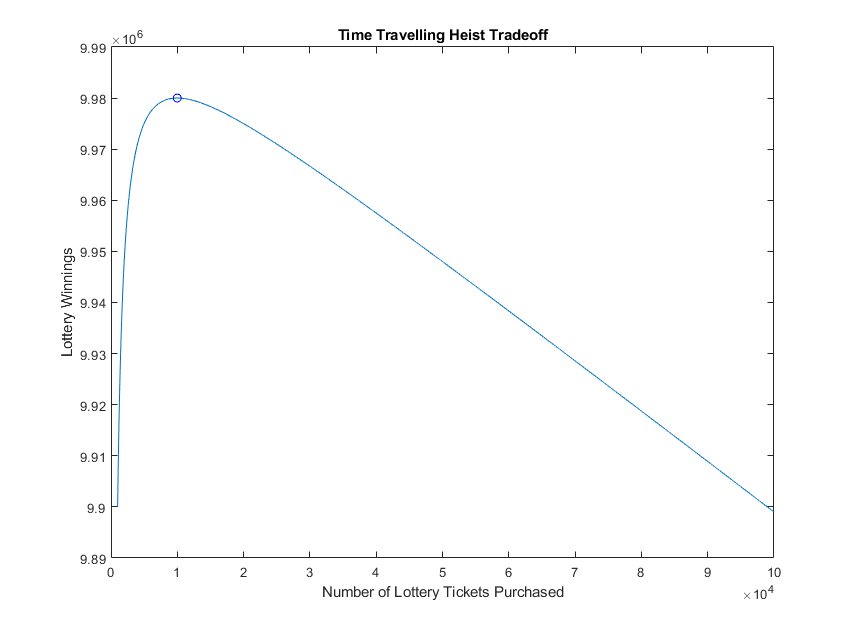
We'll use calculus to get that exact value:
\begin{align} f(x) &= 10^7 \left(\frac{x}{10+x}\right) - x \\ f'(x) &= 10^7 \left(\frac{10 + x - x}{(10+x)^2}\right) - 1 \\ &= 10^7 \left(\frac{10}{(10+x)^2}\right) - 1 \\ &= \left(\frac{10^8}{(10+x)^2}\right) - 1 \end{align}
Setting \(f'(x) = 0\) yields:
\begin{align} f'(x) &= 0 \\ \left(\frac{10^8}{(10+x)^2}\right) - 1 &= 0 \\ \frac{10^8}{(10+x)^2} &= 1 \\ 10^8 &= (10+x)^2 \\ 10 + x &= \pm 10^4 \\ x &= 10^4 - 10 \quad \text{or} \quad -10^4 - 10 \\ \end{align}
Hopefully you don't plan on winning negative amounts of money, so our optimal \(x = 10^4 - 10 = \boxed{9990}\) tickets.
We make sure that the above value actually maximizes the winnings by pluging it into the double derivative of \(f(x)\):
\begin{align} f'(x) &= \left(\frac{10^8}{(10+x)^2}\right) - 1 \\ f''(x) &= - \frac{2 \times 10^8}{(10+x)^3} \\ f''(9990) &= -\frac{2 \times 10^8}{(10+9990)^3} \\ &= -\frac{2 \times 10^8}{10000^3} \\ &< 0 \\ \end{align}
So at \(x = 9990\) the winnings function is concave down and that value is indeed the maximum. We can also see it in the graph above.
Your maximum winning is:
\begin{align} f(x) &= 10^7 \left(\frac{x}{10+x}\right) - x \\ f(9990) &= 10^7 \left(\frac{9990}{10+9990}\right) - 9990 \\ &= \boxed{9980010} \\ \end{align}
Yes, for a jackpot of 10 million, you will be taking home $9,980,010, or 99.8% of the entire jackpot share. I hope at least you treat the other 10 travellers to dinner, or something...
Here is a fun exercise. We are assuming your 10 other travelling companions are as equally smart as you, and are probably thinking of the same thing. If they all purchase 9990 tickets each, then your winning will be once again \((10M/11) - 9990\), actually losing $9,989 had you just purchased 1 ticket in the first place! So assuming other travellers plan their purchases optimally, can you do better than splitting the share? If so, what is the point where you or anyone else, can no longer do better (i.e. reaching the Nash Equilibrium)?
The idea is that here you would not even imagine purchasing 9990 tickets, because you cannot assume your companions will each purchase 1 ticket. Instead, you would assume your companions will each purchase \(x\) tickets. We are assuming, of course, that your companions will each think the same and the problem is symmetric. For the equilibrium, you will also be purchasing \(x\) tickets because if you purchase a different amount, your companions will adjust the equilibrium amount accordingly to optimize their earnings. In the end, denoting your winnings to be once again \(f(x)\), we have:
\begin{align} f(x) &= 10^7 \left(\frac{x}{10x+x}\right) - x \\ &= 10^7 \left(\frac{x}{11x}\right) - x \\ &= 10^7 \left(\frac{1}{11}\right) - x \\ \end{align}
The optimal value for you is clearly \(x = 1\), or only purchasing 1 ticket. If you try to move this equilibrium value up by purchasing more tickets, others will think the same, therefore maintaining the equal share of the jackpot and the only thing you are increasing is the purchasing cost. Therefore, assuming everyone acts perfectly logically, what realistically happens is that everyone will be buying exactly 1 ticket and split the winnings while minimizing the purchasing cost.