Riddler Express: October 15, 2021

David Ding

October 17, 2021

Ballpark Figures

Explanation:

First of all, I love those team names! Riddler League Baseball fans must also be fans of math as well. Some other team ideas I had were:

LA Angles

— David Ding (@DavidYiweiDing) October 15, 2021

Alright, cheesy team names apart, let's tackle the actual puzzle. I will do this by solving a more general case, which asks the question: on average, how many games will the series last if the Tampa Bay Lines have a probability of $p$ to win each game? The answer to the original problem would be when $p=0.5$.

Before delving into the problem, let me clearly outline a few assumptions:

• Each game's outcome is independent of the others.
• Each team's win probability for every game is constant. That is, for Tampa Bay Lines it is $p$ and for the Minnesota Twin Primes, it is $q=1-p$.
• Each team's win probability also remains unchanged for the duration of any game.

There are many ways to solve the problem given the above assumptions, including using a Markov Chain with an unsightly number of states and transitions. Since we are only interested in the number of games played and not the actual probability, we can simply the solving process by making a key observation:

The series ends in $n$ games if the winning team wins the $n$th game while having won 3 out of the past $(n-1)$ games, for $4\le n\le 7$.

At the first glance, it might seem that the above statement is not robust, as there could be opportunities for counterexamples or double counting. However, in fact, the observation is quite foolproof. For one thing, there is no way for the losing team to win 4 games out of the past $(n-1)$ games if the winning team already won 3, because $4\le n\le 7$. Even as $n=7$, the most games the losing team could've won is 3, and so if the winning team takes game $n$ then only that team can win the series. The second doubt regarding double-counting scenarios is in fact unwarranted, as there is no way for the same situation to be counted twice. The main reason is that while there are many ways for a team to win 3 out of $(n-1)$ games, only one scenario can be established if game $n$ is a series-clinching one. For example, consider two scenarios, where in the first the winning team wins the series in 5 games and in the latter 6 games. Say in both cases that team is up 3-1 through 4 games. Well, the difference is game 5. In the first case the winning team would win that game and clinch the series, whereas in the latter case that team must lose game 5 so that game 6 is the series-clinching one. In both cases, the sequences of victories are necessarily different in the end to ensure the specific games in the series, even if the beginnings are identical.

Therefore, we can go ahead and translate the above observation into the language of mathematics. Let $f_p(n)$ denote the probability that Tampa Bay Lines clinch series in $n$ games with each game's win probability being $p$. Let's look at $f_p(n)$. From our observation, we have:

$$\begin{array}{rl}& f_p(n)\\ & =P(\text{T wins game n}|\text{T wins 3 out of past (n-1) games})\\ & \times P(\text{T wins 3 out of past (n-1) games})\\ & =P(\text{T wins game n})P(\text{T wins 3 out of past (n-1) games})\\ & =P(\text{T wins game n})P(\text{T wins 3 out of (n-1) games})\\ & =pP(\text{T wins 3 out of (n-1) games})\end{array}$$

The last lines are from the independence assumption we made about the problem setup. The probability that Tampa Bay Lines win 3 out of $(n-1)$ games can be modelled with binomial distribution. Continuing our derivation on $f_p(n)$, we have:

$$\begin{array}{rl}& f_p(n)\\ & =pP(\text{T wins 3 out of (n-1) games})\\ & =p(\genfrac{}{}{0ex}{}{n-1}{3})p^3{q}^{(n-1)-3}\\ & =(\genfrac{}{}{0ex}{}{n-1}{3})p^4{q}^{n-4}\end{array}$$

By symmetry, the probability that Minnesota Twin Primes clinch the series in $n$ games is:

$$\begin{array}{r}(\genfrac{}{}{0ex}{}{n-1}{3})q^4{p}^{n-4}\end{array}$$

Let $g_p(n)$ denote the probability that the series ends in $n$ games given the win probability for each game for Tampa Bay Lines is $p$. We have:

$$\begin{array}{r}{g}_p(n)=(\genfrac{}{}{0ex}{}{n-1}{3})(p^4{q}^{n-4}+q^4{p}^{n-4})\end{array}$$

As reminder, $q=1-p$.

We now have an expression to denote the expected number of games:

$$\begin{array}{rl}& \text{Expected Number of Games}\\ & =\sum _{n=4}^{7}n{g}_p(n)\\ & =\sum _{n=4}^{7}n(\genfrac{}{}{0ex}{}{n-1}{3})(p^4{q}^{n-4}+q^4{p}^{n-4})\\ & =\sum _{n=4}^7\frac{n(n-1)!}{3!(n-4)!}(p^4{q}^{n-4}+q^4{p}^{n-4})\\ & =\boxed{{\displaystyle 4\sum _{n=4}^7(\genfrac{}{}{0ex}{}{n}{4})(p^4{q}^{n-4}+q^4{p}^{n-4})}}\end{array}$$

In particular, the solution to the original puzzle is when $p=q=0.5$, for which the above expression further simplifies:

$$\begin{array}{rl}& \text{Expected Number of Games For Evenly-Matched Teams}\\ & =\sum _{n=4}^{7}n{g}_{0.5}(n)\\ & ={4\sum _{n=4}^7(\genfrac{}{}{0ex}{}{n}{4})(p^4{q}^{n-4}+q^4{p}^{n-4})|}_{p=q=0.5}\\ & =8\sum _{n=4}^7(\genfrac{}{}{0ex}{}{n}{4})\left({0.5}^n\right)\\ & =8({0.5}^4+5({0.5}^5)+15({0.5}^6)+35({0.5}^7))\\ & =8(\frac{1}{16}+\frac{5}{32}+\frac{15}{64}+\frac{35}{128})\\ & =8\left(\frac{8+20+30+35}{128}\right)\\ & =\boxed{{\displaystyle \frac{93}{16}}}\\ & =5.8125\end{array}$$

Simulation Verification of Theoretical Results

We can also simulate the scenario for different values of $n$ using Monte-Carlo, and compare with our theoretical result. The simulation is done via MATLAB in a Monte-Carlo fashion with 10 million trials per value of $p$:

   
function numGames = monteCarloGames(p)
    % Given the probability of winning in p, get the expected number of
    % games in monte-carlo fashion

    numTrials = 1e7;
    sumGames = 0;
    for k = 1:numTrials
        sumGames = sumGames + monteCarloHelper(p);
    end

    numGames = sumGames / numTrials;
end

function numGames = monteCarloHelper(p)
    % One trial of series
    aWin = 0;
    bWin = 0;
    numGames = 0;

    while aWin < 4 && bWin < 4
        if rand < p
            aWin = aWin + 1;
        else
            bWin = bWin + 1;
        end

        numGames = numGames + 1;
    end
end
		

This yields the following result:

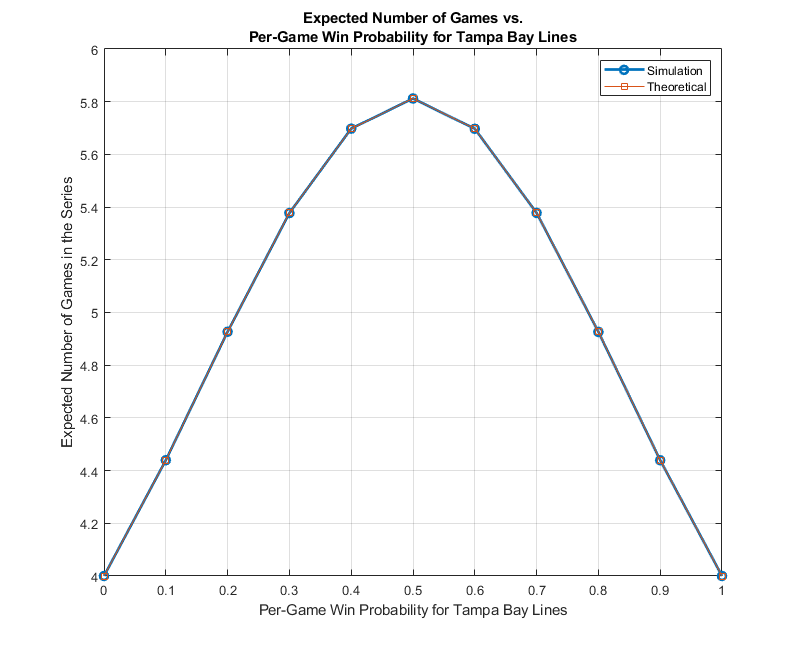
As one can see, the simulation is pretty close to our theoretical result. Furthermore, we can remark on several insights obtained from the graph. Namely:

• The graph is symmetric about $p=0.5$. This is not surprising as when only considering the number of games played, one team's advantage is another's disadvantage, and so the expected number of games should be the same when say $p=0.2$ as when $p=0.8$.
• The expected number of games peaks at $p=0.5$. An intuitive explanation is that a series would end quickly if one team is dominating the other, leading to possible sweeps or 4-1 victories. Only when both teams are evenly matched can we have an exciting series with the maximum expected number of games.
• The expected number of games as the teams become more and more lopsided goes to 4, as expected since then it would become very plausible for the dominating team to sweep the other in the best-of-seven series.

Let's have one more interesting observation. Let's calculate the probability that the series will go into 7 games for two evenly-matched teams. That would be:

$$\begin{array}{rl}& \text{Probability of Series Going 7 With Two Evenly Matched Teams}\\ & =g_{0.5}(7)\\ & ={(\genfrac{}{}{0ex}{}{n-1}{3})(p^4{q}^{n-4}+q^4{p}^{n-4})|}_{p=q=0.5,n=7}\\ & =2(\genfrac{}{}{0ex}{}{6}{3})\left({0.5}^7\right)\\ & =\frac{40}{128}\\ & =\boxed{{\displaystyle \frac{5}{16}}}\\ & =0.3125\end{array}$$

Interestingly enough, for MLB, there have been 116 World Series played, of which 40 have reached seven games. That's a game-seven rate of 0.345, which is comparatively close to the evenly matched scenario presenting by two battling teams from Riddler League Baseball. Looks like whether we are in RLB or MLB, some things don't ever change!