



December 25, 2020
From Tinbergen Institute comes a holiday puzzle perfect for Christmas Day: (Courtesy of Prof. Henk Tijms)

(Paraphrased) "Suppose you are one of 10 board members called upon by Saint Nicholas to undo the evil intent of the Crazy Santa Claus hoarding educational games from being delivered as Christmas presents, devise a decision rule that would ensure you can save Christmas! You and the nine other associates are placed in separate rooms with no communication nor prior planning, and you have a fair coin in your hand. Now, in order to save Christmas, you must:
In other words, the evil Santa Claus has decreed that at least one of you must toss the coin, and all those who toss their coins MUST all get heads as a result. One tail or if no one tosses his/her coin means those educational games will forever be hoarded by Santa. How would you proceed to maximize your chances of success? Remember, no communication nor prior planning of any kind is allowed with any other associates."
At first glance, this seems hopeless. There is an obvious trade-off on whether you should toss the coin or not. If you decide to toss the coin, you decrease the probability that all tossed coins must come up heads as each coin toss is independent of one another. It is not hard to see that if \(k\) associates toss their coins, the probability of success would be \(\left(\frac{1}{2}\right)^k\) which decays to 0 as \(k\) increases. On the other hand, suppose each associate thinks that way, no one would end up tossing their coins, which would fail the mission anyways!
Only if there is prior planning, where one of the associates can be the "designated tosser", then there would be a 50% chance of success. If only....
Well, we make do with what we've got. Since we cannot plan ahead, we will all agree, in our own heads as we are pro logicians, a probability \(p\) that denotes the probability each of the associates will toss his/her coin. What is that magical \(p\) that would maximize the chance of undoing Crazy Santa's evil plan?
Let's solve for the general case first and specialize later. Suppose there are \(N\) associates, of which \(k\) ended up tossing the coins. As mentioned earlier, the probability of success then would be \(\left(\frac{1}{2}\right)^k\) as we are assuming fair coins and independent tosses here. However, what is the probability that we will have \(k\) tossers among the \(N\) associates? Let \(X\) be the random variable representing the number of tossers. It is not hard to see that \(X\) is a binomial random variable with parameters \(N\) and \(p\). This is because no prior planning is allowed so each associate would each have the same probability of \(p\) of tossing the coin, independent of other associates. Sum of \(N\) independently and identically distributed (i.i.d.) Bernoulli random variables yields a binomial one.
Therefore, we can write out the PMF of \(X\) as follows: \begin{equation} P_X(X = k) = \binom{N}{k} p^k (1-p)^{N-k}, \quad k = 0, 1, \dots, N \end{equation}
The probability of success, given the rules of the game decreed by Santa, would therefore be: \begin{align} P(\text{Success}) &= \sum_{k=1}^N P(\text{Success} | k \text{ tossers}) P(k \text{ tossers}) \\ &= \sum_{k=1}^N \left(\frac{1}{2}\right)^k P_X(X = k) \\ &= \sum_{k=1}^N \left(\frac{1}{2}\right)^k \binom{N}{k} p^k (1-p)^{N-k} \end{align}
We now have an expression in terms of the variable that we want to optimize, \(p\), and the parameter \(N\), albeit it is an ugly expression. We can simplify the equation by realizing that our expression is simply \(\mathbb{E}\left[\frac{1}{2}^X\right]\). If this expression looks familiar, that is because is very close to the definition of the characteristic function . Recall that the characteristic function of the binomial random variable is: \begin{equation} \mathbb{E}\left[e^{itX}\right] = (1 - p + pe^{it})^N \end{equation}
We can simply replace \(e^{it}\) with \(\frac{1}{2}\). Of course, we must be careful as our expression for probability of success sums \(k\) from 1 to \(N\), whereas the support of \(X\) goes from 0 to \(N\). Therefore, we must take care of the \(k = 0\) case, which simplifies to \((1-p)^N\). Combining this with the "modified" characteristic function yields an expression for probability of success: \begin{align} f(p) &= \left(1 - p + \frac{p}{2}\right)^N - (1-p)^N \\ &= \left(1 - \frac{p}{2}\right)^N - (1-p)^N \end{align}
Let's visualize our family of functions with various values of \(N\):
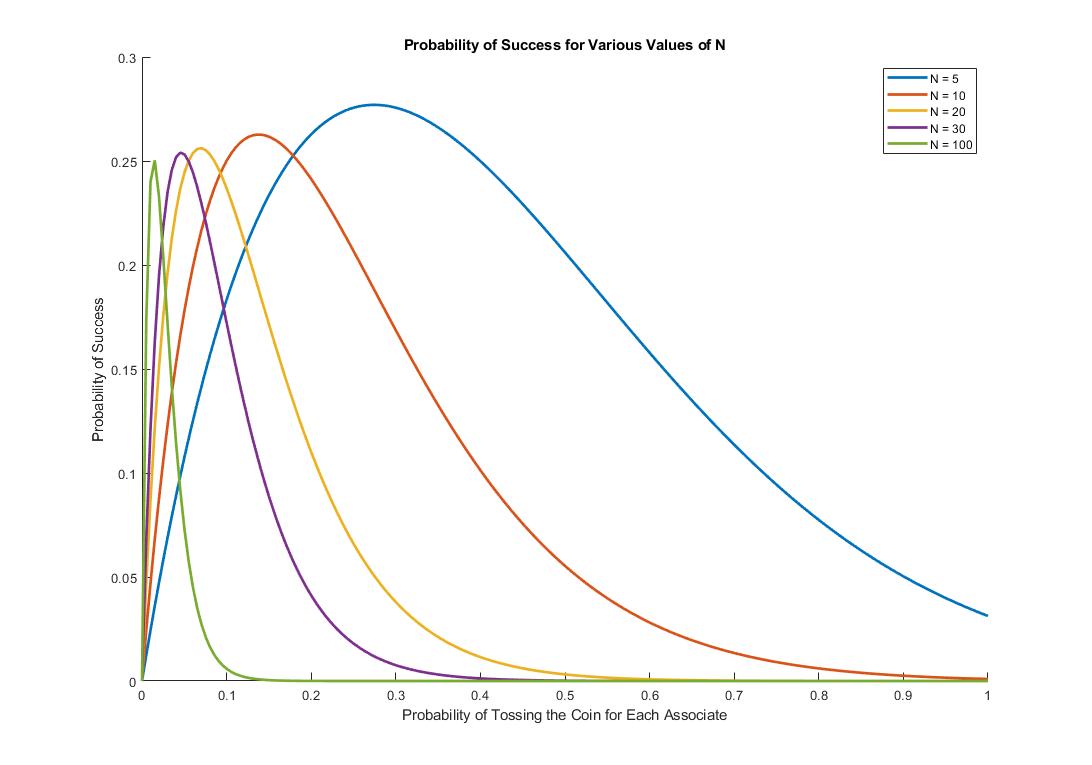
Looks like for each values of \(N\) provided, for \(0 \le p \le 1\) we have a global maximum. We can therefore take the derivative of our \(f(p)\) with respect to \(p\) to get an optimal value. The derivative-taking should be very straightforward:
\begin{align} f'(p) &= N\left[(1-p)^{N-1} - \frac{1}{2}\left(1 - \frac{p}{2}\right)^{N-1}\right] \end{align}
Setting \(f'(p)\) to 0 and realizing that \(N > 0\), we must have: \begin{align} (1-p)^{N-1} - \frac{1}{2}\left(1 - \frac{p}{2}\right)^{N-1} &= 0 \\ (1-p)^{N-1} &= \frac{1}{2}\left(1 - \frac{p}{2}\right)^{N-1} \end{align}
Substituting \(N = 10\) for our original problem, and we get the optimal \(p^* \approx 0.136\). Substituting this value into our original function for probability of success yields: \begin{equation} \boxed{f(p^*) = \left(1 - \frac{p^*}{2}\right)^{10} - (1-p^*)^{10} \approx 0.262} \end{equation}
As N gets larger and larger, it's easy to see that \(p^* \to 0\). This would happen for very large \(N\). Intuitively, this would imply that as the number of associate increases, each associate would become more and more conservative when it comes to whether or not to toss the coin. For \(N = 100\), we would get: \begin{equation} \begin{cases} p^* \approx 0.015 \\ f(p^*) \approx 0.25 \\ \end{cases} \end{equation}
For N being very large, even a powerful computational program like Matlab will spit out that \(f(p^*) \to 0\) for very small values of \(p^*\) due to limits of data precision. However, does \(f(p^*)\) truly go to 0 or rather to some other asymptotic value, as seen above perhaps to \(\frac{1}{4}\)? Let's find out next!
Prof. Henk Tijms pointed out an insightful trend on this interesting Crazy Santa puzzle in the limit that Saint Nicholas has a very, very large army of associates (i.e. the case where \(N \to \infty\)).
As seen in my post about the fascinating connections between statistic models, if \(X \sim \text{bin }(N, p)\), for large values of \(N\), \(X\) can be approximated by a Poisson random variable such that \(X \sim \text{Poisson }(\lambda = Np)\). If we plug our new model into our original expression for probability of success, we would get:
\begin{align} P(\text{Success}) &= \sum_{k=1}^\infty P(\text{Success} | k \text{ tossers}) P(k \text{ tossers}) \\ &= \sum_{k=1}^\infty \left(\frac{1}{2}\right)^k P_X(X = k) \\ &= \sum_{k=1}^\infty \left(\frac{1}{2}\right)^k \frac{e^{-\lambda} \lambda^k}{k!} \end{align}
Where the last part of the last line is the PMF of the Poisson distribution. Again, realizing the fact that the last line is simply \(\mathbb{E}\left[\frac{1}{2}^X\right]\) minus the \(k = 0\) bit, we first note the characteristic function of the Poisson Distribution: \begin{equation} \mathbb{E}\left[e^{itX}\right] = e^{\lambda (e^{it} - 1)} \end{equation} Then we replace \(e^{it}\) with \(\frac{1}{2}\), and noting that for the \(k = 0\) case we get \(e^{-\lambda}\) and so we obtain: \begin{align} P(\text{Success}) &= f(\lambda) \\ &= e^{\lambda \left(\frac{1}{2} - 1\right)} - e^{-\lambda} \\ &= e^{-\frac{\lambda}{2}} - e^{-\lambda} \end{align}
To simply the optimization process here, we will use a change of variable to let \(x = e^{-\frac{\lambda}{2}}\). This means the probability of success reduces down to: \begin{equation} f(x) = x - x^2 \end{equation} That is, a concave quadratic function, for which setting 0 to its derivative we obtain: \begin{align} 0 &= f'(x) \\ 0 &= 1 - 2x \\ x^* &= \frac{1}{2} \end{align}
Hence, \(f(x^*) = \frac{1}{2} - \left(\frac{1}{2}\right)^2 = \frac{1}{2} - \frac{1}{4} = \frac{1}{4}\). That is, as \(N \to \infty\), the probability of success indeed converges to \(\frac{1}{4}\).
For the optimal probability of each associate tossing the coin, \(p^*\), we simply unwind our variable substitutions: \begin{align} p^* &= \frac{\lambda^*}{N} \\ &= \frac{2\log\left(\frac{1}{x^*}\right)}{N} \\ &= \frac{2\log(2)}{N} \\ \end{align}
As to how the associates will simulate in their heads the \(p^*\) needed to decide whether or not to toss the coin, we'll leave that to the magic of the Holiday Season!